Cel bloga

Celem tego kursu jest wprowadzenie do praktyki eksploracji danych i uczenia maszynowego. Zawarte materiały należy traktować jako pierwszy krok do tej tematyki z zastosowaniem w praktyce prostych powszechnych narzędzi jak Excel, a dla bardziej zainteresowanych przedstawiona będzie możliwość zastosowania nabytej wiedzy w Java z wykorzystaniem algorytmów różnych bibliotek ze szczególnym uwzględnieniem biblioteki WEKA. Będzie też trochę matematyki, ale w zakresie jedynie koniecznym do zrozumienia danej metody rozwiązującej konkretny problem.

Eksploracja danych jest połączeniem stosowanych statystyk, logiki, sztucznej inteligencji, uczenia maszynowego i systemów zarządzania danymi. Nie jest wymagane duże doświadczenie w tych dziedzinach, aby korzystać z materiałów zawartych w tym blogu. Większość oferowanych źródeł i kursów do nauki Data Mining lub Machine Learning proponuje wykorzystanie takich programów jak RapidMiner, a dla Machine Learning programowanie w języku Pyton. Na tym blogu nie idziemy pod prąd, ale algorytm zrozumiemy wtedy, gdy zainicjujemy go krok po kroku, więc w miarę możliwości będziemy korzystać z Excel lub wizualizacji WEKA. Jeśli chodzi o Machine Learning to bazujemy na Java, główny powód, to możliwość wykorzystania dostępnych zestawów algorytmów WEKA jako możliwość stosowania w aplikacjach Javy i SPRING’a.

Co będzie potrzebne:

• Zainstalowany pakiet MSOffice z arkuszem kalkulacyjnym Excel, niestety płatny, ale można skorzystać ze starych wersji
• Zainstalowana Java 1.8 lub wyższa plus edytor np. darmowa wersja IntellJ IDEA Educational, resztę potrzebnych bibliotek dołączymy korzystając z Maven
• Zainstalowany pakiet algorytmów WEKA Waikato University Hamilton, New Zealand, pakiet jest darmowy. Do prób kontrolnych poza JAVA.

Ponadto możemy praktycznie przyjąć za pewnik dwa dogmaty:

• Wszystko co sam wymyślisz pewnie już tu jest https://stackoverflow.com/
• Jeśli jest biblioteka konkretnych algorytmów ML/AI napisana w innym języku to jest także jej odpowiednik dla Java. Algorytmy uczenia maszynowego są często najpierw tworzone w laboratoriach uniwersyteckich, w wielu językach, takich jak skrypty Shell, Python, R, MATLAB, Scala lub C ++, aby utworzyć nową koncepcję i teoretycznie przeanalizować jej właściwości. Java jest to de facto język korporacyjny, co można przypisać statycznemu typowaniu, solidnej obsłudze IDE, dobrze zdefiniowanej strukturze wzorców,i metod testowania, a także posiada przyzwoity model obsługi wątków oraz współbieżne biblioteki struktur danych o wysokiej wydajności. Konkretny algorytm może przejść długą drogę do końcowej refaktoryzacji, ale możemy przyjąć za pewnik, że prędzej czy później pojawi się w Java.

Podstawowe informacje o danych

Podział danych jest stosunkowo prosty. Dane dzielimy zasadniczo na dwa podstawowe modele tj. dane podstawowe oraz dane drugorzędne.

Dane podstawowe

Dane podstawowe są to dane które występują w swojej rzeczywistej postaci (takiej w jakiej je pozyskano) beż żadnych modyfikacji dostosowujących do dalszych obliczeń i analiz. Dane podstawowe zbierane są za pomocą różnych metod których przykłady przedstawiono poniżej:

1.      Wywiad

Dane zbierane w trakcie tego procesu pochodzą z wywiadu z odbiorcami docelowymi przez osobę zwaną ankieter, a osoba, która odpowiada na wywiad, jest znana jako osoba przeprowadzająca wywiad.

2.      Ankieta

Ankieta to w zasadzie proces badawczy, w którym zadaje się listę odpowiednich pytań, a odpowiedzi są zapisywane w formie tekstu, dźwięku lub wideo.

3.      Eksperyment

Eksperyment to sposób zbierania danych poprzez przeprowadzanie eksperymentów, badań i śledztw oraz odpowiednim zapisywaniu obserwacji i atrybutów obserwacji. Stosuje się różne metody prowadzenia eksperymentów, istotne jest jednak to jakie wartości są elementami obserwacji i atrybutów. Mogą to być np. wartości tekstowe, obiektowe, liczbowe, logiczne mieszane.

Dane wtórne

To szczególny typ danych które zostały zebrane i innych powodów zostały zarejestrowane i mogły być poddane pewnym modyfikacjom koniecznym do ich analizy lub wynikającymi ze specyfiki ich źródła generowania. Ogólnie dane wtórne dzielimy na:

1.      Dane organizacyjne

Ogólnie można przyjąć, że są to dane wynikające z działalności związanej z jakimś przedsięwzięciem. Mogą to być zapisy rynkowe, zapisy sprzedaży, transakcje, dane klientów, zasoby księgowe itp. Należy przy tym zauważyć, że koszt i czasochłonność przy pozyskiwaniu danych ze źródeł organizacyjnych jest stosunkowo niskie, wynika to po prostu z faktu, iż są one z reguły koniecznością lub wymogiem przy realizacji szeroko rozumianego przedsięwzięcia, np. bank prowadzi informacje o klientach w ramach polityki kredytowe itp.

2.      Dane zewnętrzne

Ten typ danych jest elementem pochodnym działalności organizacyjnej wynikającym z samej działalności lub elementem niezbędnym do realizacji działalności. Przykładowe to np. odczyty liczników prądu mające wpływ na koszty działalności, ale fakturę otrzymujemy z od dystrybutora energii zgodnie z jego taryfikatorem. Mogą to też być statystyczne dane rządowe [GUS] mające wpływ na marketing firmy lub przedmiot działalności.

Podstawowe kategorie źródeł wydobywanych danych

1.      Sety – zestawy danych płaskich lub pliki płaskie

Przykładem setu są np. dane pomiarowe jakiegoś eksperymentu w postaci pliku CSV gdzie w mamy atrybuty w postaci kolumn, argumenty i wartość wyniku/wyników dla argumentu. Set nie posiada żadnych relacji do innych tabel. Dane mogą mieć postać tekstową liczbową lub logiczną i można je wyodrębnić za pomocą algorytmów eksploracji, które przyjmiemy do ich zastosowania. Przykład – algorytm po wczytaniu pliku kasuje wiersze z wynikiem „0” ponieważ jest to wynik błędu transmisji jakichś danych

2.      Relacyjne bazy danych

Bazy danych które posiadają tabele powiązane relacjami. Najczęściej posługujące się standardowym API  w postaci  „sequel” (Structured Query Language). W takich bazach kopanie danych nie jest łatwe, wymaga bowiem znajomości SQL. Należy pamiętać, że jest to tzw. zbiór danych zorganizowanych zarówno danych w tabeli pod względem uporządkowania według ID tabeli jak i również zdefiniowanych relacji pomiędzy tabelami. Należy zauważyć, że relacyjne bazy danych są relatywnie dość „ciężkim” tematem do kopania danych ze względu na swoją relacyjną strukturę i bardzo często taki zestaw danych poddaje się przetworzeniu do postaci „setu” gdzie w wiersze stanowią tzw. obserwacje a w kolumny atrybuty

3.      Hurtownie danych ang. DataWarehouse

Hurtownie danych to nic innego jak zbiory danych zintegrowanych z wielu źródeł, który będzie służył zapytaniom i podejmowaniu decyzji. Zasadniczo wyróżniamy trzy typy hurtowni danych: hurtownia danych jako przedsiębiorstwa [Enterprise DataWarehouse] , hurtownia danych skompilowana do mniejszego rozmiaru zdefiniowanych wcześniej danych zwana magazynem danych [Data Mart] i hurtownia wirtualna [Virtual Warehouse]

4.      Dane Transakcyjne lokowane w bazach danych np. eXtremeDB

Dość ważny element zbiorów danych. Częstym elementem kreowania tego typu danych jest wykorzystanie np. w SPRINGu wzorca ACID – klasy transakcji. Oznacza to zapis do bazy danych elementu transakcji, uporządkowanego wg znacznika czasu i daty (szeregów czasowych) z cechami Jednoznaczności, Spójności, Izolacji, Trwałości

• Atomic
• Consistency
• Isolation
• Durability

w powiązaniu z obiektem transakcji jak operacja giełdowa, bankowa, przyjęcia wydania z magazynu. To co należy zapamiętać to zasadę, że na tym samym obiekcie nie można wykonywać wielu transakcji w tym samym czasie. Przykład: na budowie w biurze A osoba chce pobrać np. to samo narzędzie co inna osoba w biurze B. Nie można wypożyczyć tej samej rzeczy w tym samym czasie przez dwie różne osoby. Tak więc np. jeśli biuro A było pierwsze w wątku biuro B będzie czekało na wynik transakcji i zobaczy jedynie status po operacji, że narzędzie jest już wypożyczone lub nie (jeśli np. odstąpiono od wypożyczenia w biurze A)

5.      Multimedialne bazy danych np Netflix

Wszelkie zbiory danych multimedialnych jak filmy, nagrania muzyczne wraz z ich systemem ewidencji danych klientów, pobrań  itd. Ważnym elementem tych baz są dane ewidencyjne i obrotu multimediów pozwalające na kopanie danych w celu przyjęcia właściwej strategii marketingowej czy kompletacji ofertowej.

6.      Topograficzno-Przestrzenne bazy danych np. OpenStreet

Przykładem takich danych jest ogólnie dostępna baza społecznościowa OpenStreet. Istotne dla kopania danych są nie tylko dane topograficzne, ale zawarte w różnych warstwach dane o elementach obiektów budowlanych, zmianach przestrzennych w czasie, POI itd.

7.      Sieć strony WWW

Najbardziej dynamiczne i heterogeniczne repozytorium. Odnosi się do World Wide Web to zbiór dokumentów i zasobów, takich jak audio, wideo, tekst itp., które są identyfikowane przez jednolite lokalizatory zasobów (URL) za pośrednictwem przeglądarek internetowych, połączone za pomocą stron HTML i dostępne za pośrednictwem sieci internetowej.

Data Mining, Kopanie Danych, Eksploracja Danych, KDD – Knowledge Discovery from Databases

Eksploracja danych to dyscyplina związana z pozyskiwaniem danych, ich przygotowaniem (czyszczenie, szorowanie) i metodycznym przeszukiwaniu wzorców wraz z ich analizą. Przez większość czasu nawet nie zauważamy, że to się dzieje. Przykładowo, ilekroć rejestrujemy się w celu uzyskania karty sklepowej w sklepie spożywczym, dokonujemy zakupu za pomocą karty kredytowej lub surfujemy po Internecie, generujemy dane. Dla przypadku wspomnianego powyżej beneficjentami naszych działań jest market, który rejestruje nasze dane personalne i dane o zakupionym towarze, bank, który dowiaduje się co kupujemy, gdzie kupujemy i kiedy kupujemy a Gogle skrzętnie profilują nasze poczynania w sieci. Dane te są przechowywane w dużych zbiorach na potężnych serwerach należących do firm, z którymi na co dzień mamy do czynienia. W tych zbiorach danych leżą wzorce – wskaźniki naszych zainteresowań, naszych nawyków i naszych zachowań. Eksploracja danych pozwala ludziom zlokalizować i zinterpretować te wzorce, pomagając im podejmować bardziej świadome decyzje i lepiej obsługiwać swoich klientów. To powiedziawszy, istnieją również obawy dotyczące praktyki eksploracji danych. W szczególności grupy nadzorujące ochronę prywatności głośno opowiadają się za organizacjami gromadzącymi ogromne ilości danych, z których niektóre mogą mieć bardzo osobisty charakter.

O kopaniu danych jako dyscyplinie informatycznej zaczęto mówić, kiedy w 1999 roku kilka dużych firm, w tym producent samochodów Daimler-Benz, ubezpieczyciel OHRA, producent sprzętu i oprogramowania NCR Corp. oraz producent oprogramowania statystycznego SPSS, Inc. rozpoczęły współpracę w celu sformalizowania i ujednolicenia podejścia do eksploracji danych. Efektem ich pracy był CRISP-DM, standardowy proces CRoss-Industry dla eksploracji danych.

Mimo że uczestnicy tworzenia CRISP-DM z pewnością mieli żywotne interesy w określonych narzędziach programowych i sprzętowych, proces został zaprojektowany niezależnie od konkretnego narzędzia. Został napisany w taki sposób, aby miał charakter koncepcyjny – coś, co można było zastosować niezależnie od określonego narzędzia lub rodzaju danych. Proces składa się z sześciu etapów lub faz. W poniższym rysunku przedstawiono założenia procesu. [zaczerpnięto:  https://en.wikipedia.org/wiki/Crossindustry_standard_process_for_data_mining ]

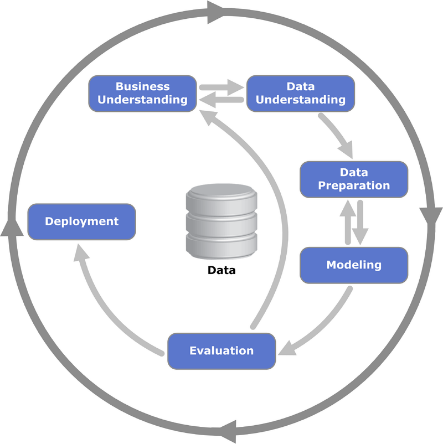
Nie ma potrzeby by znać na pamięć strukturę modelu, ale warto zaznajomić się z jego elementami opisanymi poniżej

1.      Business (Organizational) Understanding – zrozumienie potrzeb biznesowych

To jest absolutna baza do dalszych działań. Możesz wydobywać dane dniami i nocami, ale jeśli nie wiesz, czego chcesz się dowiedzieć, jeśli nie zdefiniowałeś żadnych pytań, na które trzeba odpowiedzieć, wtedy wysiłki związane z eksploracją danych będą mniej owocne. Zacznij od pomysłów na wysokim poziomie: co sprawia, że ​​moi klienci tak bardzo narzekają. Jak mogę zwiększyć marżę zysku na jednostkę? Jak mogę przewidzieć i naprawić wady produkcyjne, a tym samym uniknąć wysyłki wadliwego produktu? Jeśli zrozumiesz swojego klienta i jego oczekiwania to masz 50% sukcesu w zrozumieniu jakich danych potrzebujesz

2.      Data Understanding – zrozumienie danych

Po skorelowaniu i scentralizowaniu danych w organizacji pojawia się wiele pytań. Skąd pochodzą dane? Kto je zebrał i czy istniała standardowa metoda zbierania? Co oznaczają różne kolumny i wiersze danych? Czy istnieją akronimy lub skróty, które są nieznane lub niejasne? Bardzo często konieczne jest przeprowadzenie pewnych badań na etapie przygotowywania danych w ramach działań związanych z eksploracją danych. Czasami będziesz musiał spotkać się z ekspertami merytorycznymi z różnych dziedzin, aby dowiedzieć się, skąd pochodzą określone dane, w jaki sposób zostały zebrane oraz w jaki sposób zostały zakodowane i przechowywane. Niedokładne lub niekompletne dane mogą być gorsze niż nic w działalności eksploracji danych, ponieważ decyzje oparte na częściowych lub błędnych danych mogą być decyzjami częściowymi lub błędnymi.

3.      Data preparation – przygotowanie danych

Dane mają wiele kształtów i formatów. Niektóre dane są liczbowe, niektóre są w akapitach tekstu, a inne w formie obrazkowej, takiej jak wykresy, wykresy i mapy. Niektóre dane są anegdotyczne lub narracyjne, takie jak komentarze do ankiety dotyczącej satysfakcji klienta lub transkrypcja zeznań świadka. Nie należy jednak odrzucać danych, które nie znajdują się w wierszach lub kolumnach liczb – czasami nietradycyjne formaty danych mogą być najbardziej bogate w informacje. Przygotowanie danych obejmuje szereg czynności. Często taki proces nazywany jest czyszczenie danych lub szorowanie danych. Mogą one obejmować łączenie dwóch lub więcej zestawów danych razem, redukowanie zbiorów danych tylko do tych zmiennych, które są interesujące w danym ćwiczeniu eksploracji danych, czyszczenie danych z anomalii, takich jak obserwacje odstające lub brakujące dane, lub ponowne formatowanie danych w celu zachowania spójności.

Przykład: W pewnej ankiecie oprócz innych danych jak np. wykształcenie, wiek itd. Jest pytanie o płeć. Przedmiotem naszych badań jest korelacja grup wiekowych vs wykształcenie vs lokalizacja. W tym przypadku nie ma znaczenia czy zaznaczono płeć i taki atrybut (kolumnę) możemy pominąć, ale gdyby takie zestawienie nie dotyczyło lokalizacji, ale podziału na płeć to rezygnacja z tego atrybutu nie ma sensu natomiast wymaga analizy czy pomijamy sygnał (wiersz) z pustym polem płeć czy nie i jaką wartość błędu popełniamy.

4.      Modeling – modelowanie

Model, przynajmniej w eksploracji danych, to nic innego jak komputerowa reprezentacja obserwacji ze świata rzeczywistego. Modele to zastosowanie algorytmów do wyszukiwania, identyfikowania i wyświetlania wszelkich wzorców lub komunikatów w danych. Istnieją dwa podstawowe rodzaje lub typy modeli w eksploracji danych: te, które klasyfikują [classification] i te, które przewidują [prediction].
O klasyfikacji mówimy wtedy, kiedy dany model przypisuje pewna wartość obserwacji do konkretnej grupy.

Przykład: W układach cyfrowych TTL poziom napięcia wyjściowego to przedział 0-0,8V jest klasyfikowany jako logiczne „zero”, a poziom napięcia wyjściowego w przedziale 2,4-5,0V jest sklasyfikowany jako logiczne „1”. To co pomiędzy to stan nieustalony. Jeśli na wejście układu scalonego który jest komparatorem (np. AD8469) podamy sygnał ciągły to na wyjściu układu otrzymamy tylko możliwe dwa stany napięcia tj. poziom „0” -> 0-0,8[V] lub poziom „1” -> 2,4-5,0[V]. Ogólnie możemy to sprowadzić do postaci:

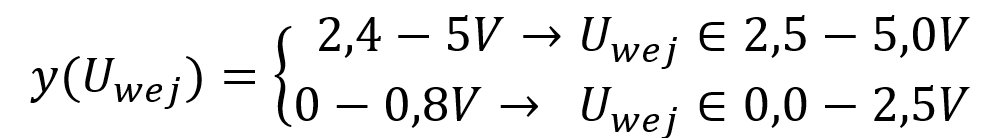
O predykcji mówimy wtedy, kiedy dany model odwzorowuje w sposób ciągły pewne zachowanie.

Przykład: Pomierzyliśmy prąd płynący przez rezystor dla kilku napięć np. 1V->1A; 2V->2A; 3V->3A. Nie znamy zależności (wzoru) pomiędzy prądem, napięciem stałym i rezystancją rzeczywista, ale chcielibyśmy wiedzieć jaka będzie odpowiedź modelu na argument o wartości 10V. Ogólnie model po obliczeniach przyjmie wartości równania dla predykcji liniowej w postaci ogólnej:

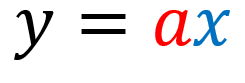
 co odpowiada w naszym przypadku równaniu prawa Ohma I= (1/R)*U

Istnieje pewne pokrywanie się między typami tych modeli wykorzystywanych do eksploracji danych. Na przykład drzewa decyzyjne. Drzewa decyzyjne to model predykcyjny używany do określania, które atrybuty danego zestawu danych są najsilniejszymi wskaźnikami danego wyniku. Wynik jest zwykle wyrażany jako prawdopodobieństwo, że obserwacja znajdzie się w określonej kategorii. Dlatego drzewa decyzyjne mają charakter predykcyjny, ale pomagają nam również klasyfikować nasze dane.

Modele mogą być proste lub złożone. Mogą zawierać tylko pojedynczy proces lub strumień albo mogą zawierać podprocesy. Niezależnie od ich układu modele są tam, gdzie eksploracja danych przechodzi od przygotowania i zrozumienia do opracowania i interpretacji

5.      Evaluation – ocena

Wszystkie analizy danych mogą zawierać fałszywe alarmy. Jednak nawet jeśli model nie daje fałszywych alarmów, model może nie znaleźć żadnych interesujących wzorców w danych. Może to być spowodowane tym, że model nie jest dobrze skonfigurowany do znajdowania wzorców, możesz używać złej techniki lub po prostu w danych może nie być nic interesującego do znalezienia przez model. Faza oceny CRISP-DM ma pomóc w określeniu, jak cenny jest Twój model i co możesz chcieć z nim zrobić.

Oceny można dokonać za pomocą wielu technik, zarówno matematycznych, jak i logicznych. Jednak poza tymi środkami ocena modelu musi również obejmować aspekt ludzki. W miarę zdobywania doświadczenia i wiedzy specjalistycznej w swojej dziedzinie będą mieli wiedzę operacyjną, która może nie być mierzalna w sensie matematycznym, ale jest niezbędna do określenia wartości modelu eksploracji danych. Korzystamy zarówno wyników obliczeń opartych na danych, jak i instynktownych technik oceny w celu określenia przydatności modelu.

6.      Deployment – wdrożenie

To ostatni etap prac. Czynności w tej fazie obejmują konfigurację automatyzacji modelu, spotkania z konsumentami wyników modelu, integrację z istniejącymi systemami zarządzania lub informacji operacyjnych, przekazywanie nowej wiedzy z użytkowania modelu z powrotem do modelu w celu poprawy jego dokładności i wydajności oraz monitorowanie i mierzenie wyniki stosowania modelu. Aby skutecznie wdrażać modele eksploracji danych, należy zachować równowagę. Dzięki jasnemu komunikowaniu funkcji i użyteczności modelu zainteresowanym stronom, dokładnemu testowaniu i sprawdzaniu modelu, a następnie planowaniu i monitorowaniu jego wdrażania, modele eksploracji danych można skutecznie wprowadzić do przepływu organizacyjnego.

Jak widzimy dane i jak je określamy

Ponieważ będziemy poruszać pomiędzy różnymi zbiorami danych omówimy nazewnictwo, z którym spotkamy się podczas naszej pracy. W różnych środowiskach danych mogą być one określane różnymi nazwami.

W relacyjnej bazie danych wiersze będą nazywane krotkami lub rekordami, a kolumny – polami.
W hurtowniach danych i zestawach danych wiersze są czasami nazywane faktami, obserwacjami, przykładami lub przypadkami, a kolumny są czasami nazywane zmiennymi, argumentami lub atrybutami. Aby zachować spójność, będziemy używać terminologii obserwacji wierszy i atrybutów kolumn.

1.      Data Set

W poniższym przykładzie przedstawiono pomiarowy plik CSV. Składa się on z dwóch atrybutów, z których jeden to argument drugi to zmienna.

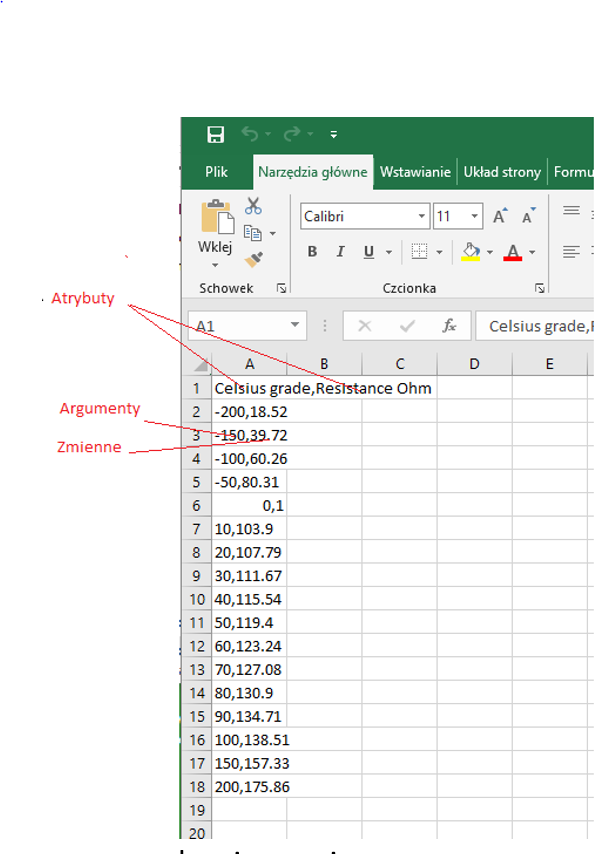
Poszczególne dane w wierszach są odseparowane przecinkami. Wartości dziesiętne są podane z separatorem kropki. Warto zwrócić uwagę na ten fakt uwagę, gdyż często dla osób poczatkujących jest to powodem wielu pomyłek. W przykładowej zależności zaznaczonej na rysunku jako argument i zmienna zależna dla wzorcowej temperatury w komorze klimatycznej:  -150^oC, zmierzona rezystancja czujnika temperatury wynosiła 39,72Ω.

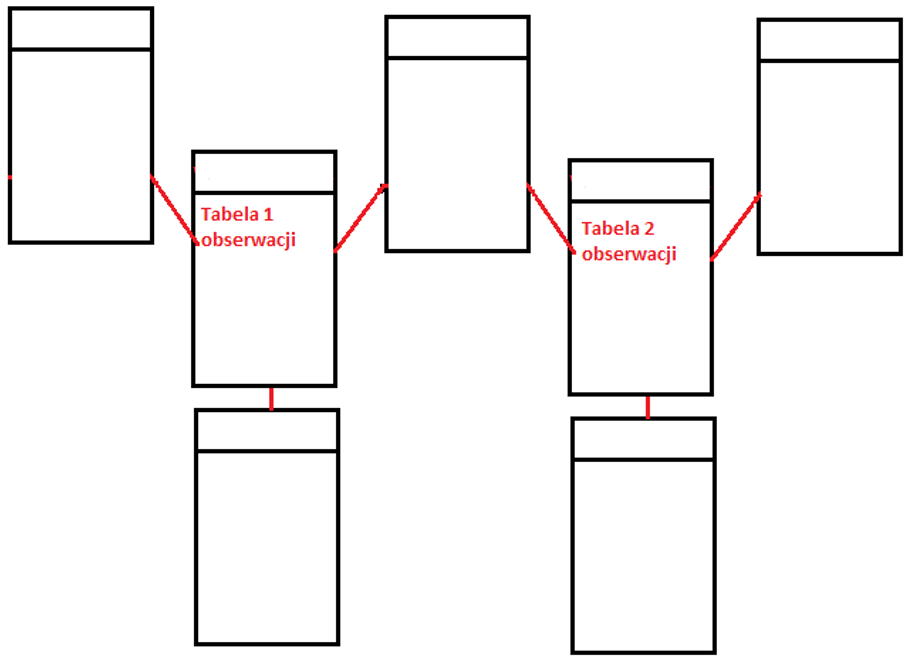
2.      Relacyjna Baza Danych

Relacyjna baza danych to zorganizowana grupa informacji w ramach określonej struktury. Kontenery bazy danych, w środowisku bazy danych nazywane są tabelami. Większość używanych obecnie baz danych to relacyjne bazy danych – są one zaprojektowane przy użyciu wielu tabel, które są ze sobą powiązane w logiczny sposób. Relacyjne bazy danych zazwyczaj zawierają dziesiątki lub nawet setki tabel, w zależności od wielkości organizacji. Załączony poniżej przykład bazy danych utworzony na potrzeby wypożyczalni samochodów pokazuje złożoność tabel i relacji

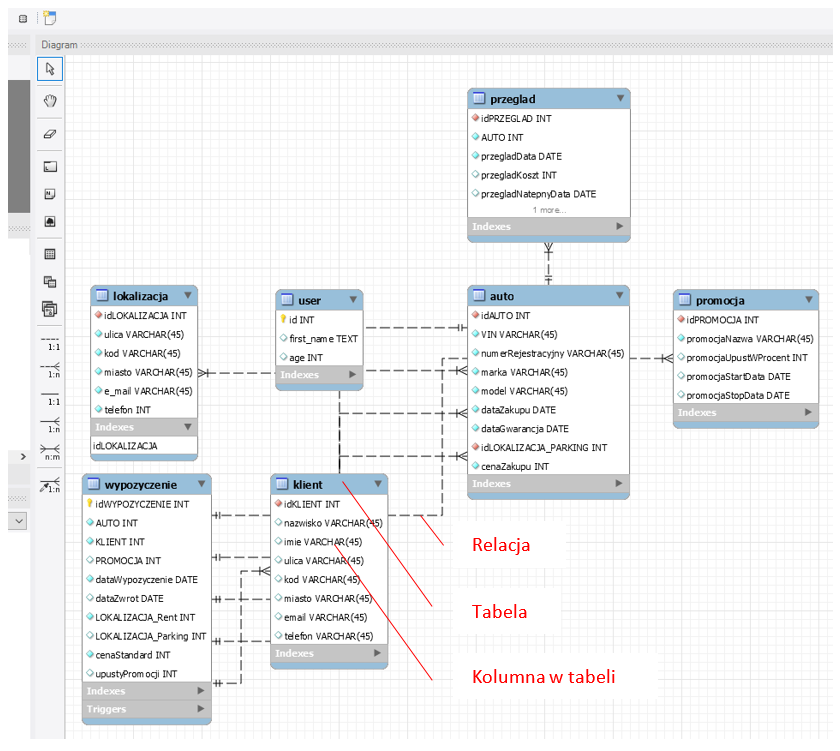
Jest to diagram gdzie każda z tabel posiada własne kolumny z atrybutami wg nazw. Jak widoczne w tabeli każda z tabel zawiera dziesiątki wierszy z danymi natomiast linie łączące tabel wskazują jakie są relacje (zależności) pomiędzy danymi w tabelach. Przykładowa tabela testowa:

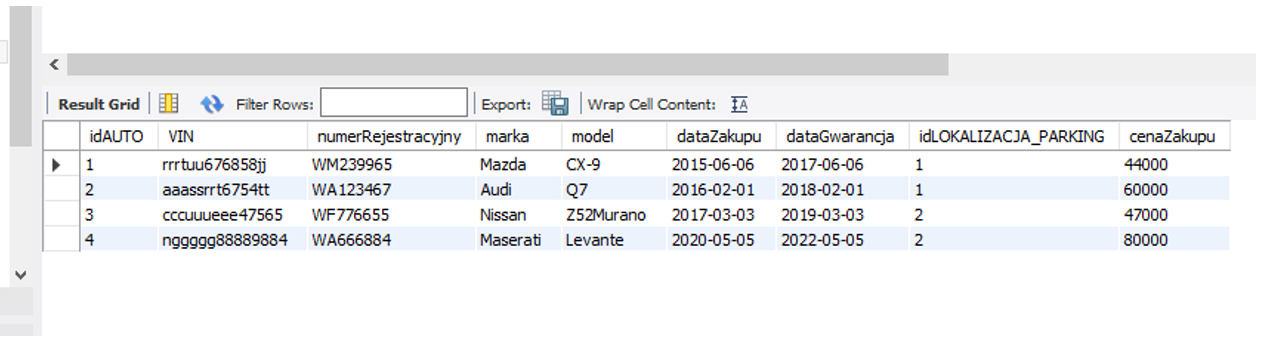
Na pierwszej pozycji od lewej jest kolumna identyfikatora idAUTO łatwo zauważyć, że ta tabela przechowuje relację do tabeli z identyfikatorem idLOKALIZACJA_PARKING to jest właśnie relacja. Większość relacyjnych baz danych, które są zaprojektowane do obsługi dużej liczby odczytów i zapisów (aktualizacji i pobierania informacji), jest określanych jako systemy OLTP (przetwarzanie transakcji online). Systemy OLTP są bardzo wydajne w przypadku czynności o dużym wolumenie, takich jak kasowanie, zapis, gdzie np. wiele pozycji jest rejestrowanych za pomocą skanerów kodów kreskowych lub pobieranych z odczytów urządzeń IoT w bardzo krótkim czasie. Jednak używanie baz danych OLTP do analizy jest generalnie mało wydajne, ponieważ aby pobrać dane z wielu tabel jednocześnie, należy napisać zapytanie zawierające łączenia. Zapytanie jest prostą metodą pobierania danych z tabel bazy danych do przeglądania wyników danych w zestawieniach, które w danej chwili interesują analityka. Zapytania są zwykle pisane w języku zwanym SQL (Structured Query Language; wymawiane jako „sequel”).

3.      Hurtownia danych

Hurtownia danych to rodzaj dużej bazy danych , która została zdenormalizowana i zarchiwizowana z bazy danych relacyjnej SQL. Denormalizacja to proces celowego łączenia niektórych tabel w jedną tabelę, mimo że może to spowodować zduplikowanie danych w niektórych kolumnach (lub innymi słowy, atrybutów). Denormalizacja to schematy wielowymiarowe, specjalnie zaprojektowane do modelowania systemów hurtowni danych. Głównym celem denormalizacji jest uproszczenie tabel zapytań do określonych celów biznesowych w połączeniu z odpowiednimi algorytmami czego nie da się osiągnąć w łatwy sposób metodami w standardzie SQL Schematy zostały zaprojektowane z myślą o unikalnych potrzebach bardzo dużych baz danych zoptymalizowanych do celów analitycznych (OLAP). Wyróżniamy głównie trzy typy schematów hurtowni danych:

• Schemat gwiazdy (Star Schema)
• Schemat płatka śniegu (Snowflake Schema)
• Schemat galaktyki (Galaxy Schema)

Ogólnie można powiedzieć, że wybór schematu zależy od tego co chcemy przetwarzać. Główne wymagania są następujące:

• Jakie są potrzeby biznesowe
• Jaki poziom ziarnistości musimy założyć – ile i jakich szczegółów potrzebujemy
• Ile potrzebujemy wymiarów – czyli ile tabel z jakimi danymi
• Jakie miary (wskaźniki) są nam potrzebne w wynikach

Schemat gwiazdy – z przykładem

                Schemat gwiazdy w hurtowni danych, w której środek gwiazdy może mieć jedną tabelę obserwacji i kilka powiązanych tabel atrybutów. Jest znany jako schemat gwiazdy, ponieważ jego struktura przypomina gwiazdę. Model danych Star Schema to najprostszy typ schematu Data Warehouse. Przykładowo chcemy przeanalizować nasza bazę wypożyczalni pod kątem klient , model wypożyczanego samochodu, czas wypożyczenia oraz jaki przynosi zysk w naszej wypożyczalni.

                Zaczynamy – przeglądając zestawienie zbiorcze z bazy SQL przyjrzyjmy się jakie tabele zawierają dane niezbędne do pozyskania naszych wskaźników:

Cel biznesowy to zmiana parku naszych samochodów oraz wprowadzenie pewnego wątku drzewa decyzyjnego w oprogramowaniu który pomoże obsłudze w decyzji któremu klientowi dać priorytet strategiczny a któremu „podziękować” w sytuacji kolizji oczekiwań.

Ziarnistość potrzebujemy dane o klient-> samochód->przychód

Atrybuty potrzebujemy tabeli o klientach, wypożyczeniach, samochodach, przychodach, promocjach

Wskaźniki ID Klienta, przychód

Centrum gwiazdy – co jest obserwacją lub prościej co jest kluczem pozostałych tabel w bazie SQL wypożyczalni powyżej? Jest to tabela wypożyczenia. Zatem, nasza gwiazda powinna wyglądać następująco:

Schemat płatek śniegu

Płatek śniegu jest ewolucją gwiazdy. W zasadzie tego typu schemat jest pochodna tradycyjnej bazy danych którą zdenormalizowano, ale optymalizacja wymusza konieczność dodatkowych tabel. Główną zaletą schematu płatka śniegu jest to, że zajmuje mniej miejsca na dysku niż odpowiadająca mu baza danych SQL. Do schematu gwiazdy dodawany jest łatwiejszy do zaimplementowania wymiar. Z powodu dodatkowego odniesienia wielu tabel wydajność zapytań jest zdecydowanie zmniejszona, schemat poglądowy poniżej.

Schemat galaktyka

Schemat galaktyki zawiera dwie tabele obserwacji, które mają wspólne tabele wymiarów. Jest również nazywany schematem konstelacji obserwacji. Ten schemat jest postrzegany jako zbiór gwiazd, stąd nazwa Galaxy Schema.

Machine Learning – uczenie maszynowe

Są trzy główne sposoby uczenia się, jak pokazano na poniższej liście:

• Supervised learning – uczenie nadzorowane
• Unsupervised learning – uczenie nienadzorowane
• Reinforcement learning – uczenie wzmocnione

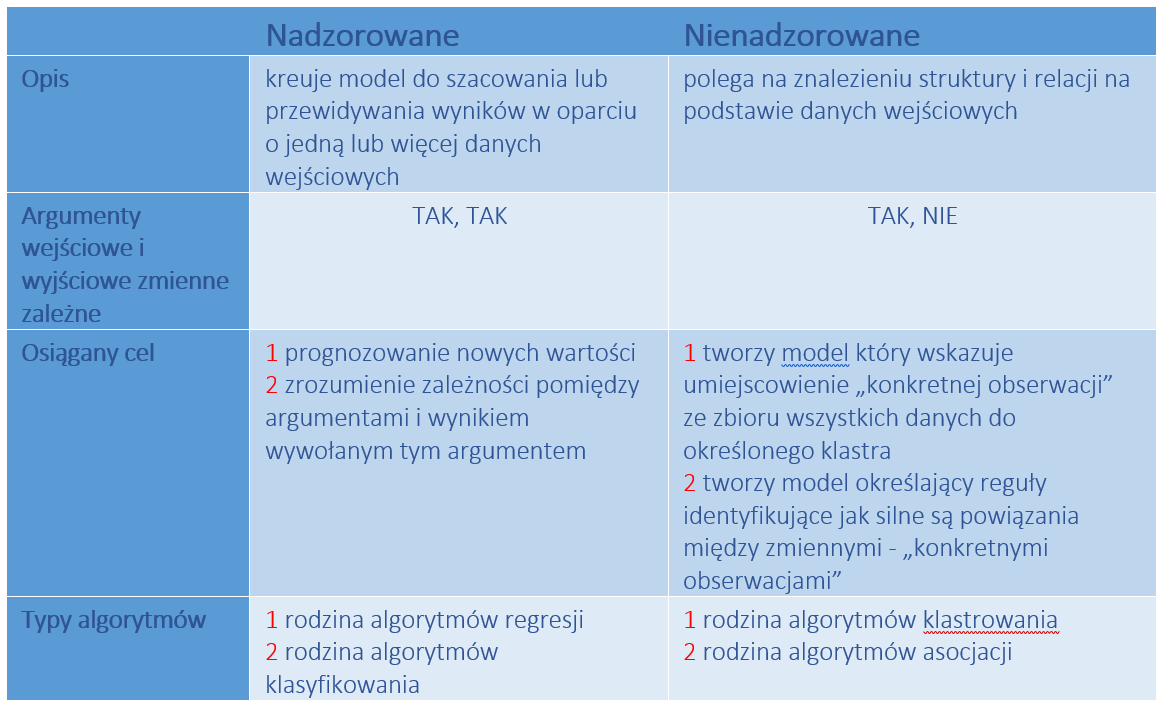
Uczenie nadzorowane

Biorąc pod uwagę zestaw przykładowych danych wejściowych x i ich wyników y, uczenie nadzorowane ma na celu nauczenie odwzorowania jako funkcja odwzorowania f, która przekształca wejścia na wyjścia w postaci funkcji

Przykład: Wykrywanie oszustw związanych z kartami kredytowymi, gdzie algorytm uczenia się jest zestawiony z transakcjami kartą kredytową (macierz X) oznaczonymi jako normalne lub podejrzane (wektor Y). Algorytm uczący się tworzy model decyzyjny, który oznacza niewidoczne transakcje jako normalne lub podejrzane (jest to funkcja f). Oczywiście by taką funkcje wyznaczyć musimy posiadać zestawu danych z hurtowni danych. W tym wypadku dwa zestawy danych tj. zestaw transakcji, które bank kolekcjonuje w swoich zasobach i zestaw danych które są oznaczone w tym banku lub w hurtowni między wieloma bankami jako oszustwo.

Wyróżniamy dwa główne typy uczenia nadzorowanego

• Regresja – zmienna wyjściowa jest ciągła np. czas rezystancja temperatura
• Klasyfikacja – zmienna wyjściowa przyjmuje konkretną sklasyfikowaną wartość np. True , False, biały, czarny

Zastosowanie:

• Predykcja (prognoza) używamy zestawu zmiennych objaśniających(argumentów), aby przewidzieć wartość jakiejś zmiennej odpowiedzi (np. dla termometru oporowego wykonaliśmy pomiary temp->rezystancja dla -5^oC; 0^oC; 5^oC; 20^oC po obliczeniu zależności R=f(temp) używając modelu [wzoru], możemy podać rezystancję termometru oporowego dla temperatury np. 100oC dla której nie wykonano pomiaru rzeczywistego)
• Wnioskowanie (inference) używamy by określić w jaki sposób zmienia się zmienna odpowiedzi, gdy zmienia się wartość zmiennych objaśniających (np. zrobiliśmy pomiary jak dla punktu powyżej, ale mamy teraz do dyspozycji omomierz i chcemy się dowiedzieć jaka mierzymy temperaturę na podstawie wskazań omomierza)

Uczenie nienadzorowane

W przeciwieństwie do nadzorowanego, nienadzorowane algorytmy uczenia się nie przyjmują podanych etykiet wyników, ale skupiają się na poznaniu struktury danych, na przykład na grupowaniu podobnych danych wejściowych w klastry. Uczenie bez nadzoru może zatem odkryć ukryte wzorce w danych.

Przykład: Algorytm rekomendacji oparty na przedmiotach, podmiotach w którym algorytm wykrywa podobne przedmioty kupione razem; na przykład osoby, które kupiły książkę A kupowały również książkę B.

Oznacza to, że nasz algorytm rozpoznaje grupy klientów, którzy mogą mieć podobne zainteresowania. Grupuje tych klientów w kategorie i proponuje zakup przedmiotów które w tej kategorii były również przedmiotem zakupów. Kupiłeś książkę kucharską na temat potraw z ryb. Jak widzi to algorytm:

1. Zalicza podmiot do kategorii gotowanie i proponuje inne książki kucharskie i dołącza reklamy marketów z żywnością itd.
2. Zalicza podmiot do kategorii wędkarstwo proponuje książki dot. wędkowanie i dołącza reklamy sklepów wędkarskich itd.
3. Zalicza podmiot jako zainteresowany wypoczynkiem nad wodą, potrawami z ryb, owoców morza i dołącza reklamy na temat zorganizowanych podróży nad morza i akweny wodne oraz reklamuje odpowiednio skonfigurowane dane o hotelach

Podsumowując, algorytm uczenia się bez nadzoru może być użyty, gdy mamy listę zmiennych (X1, X2, X3,…, Xp) i chcielibyśmy po prostu znaleźć podstawową strukturę lub wzorce w danych. Wyróżniamy dwa główne typy uczenia nienadzorowanego

• Grupowanie (Clustering) używając tego typu algorytmów, próbujemy znaleźć „skupiska” obserwacji w zbiorze danych, które są do siebie podobne.
• Skojarzenie (Association) używając tego typu algorytmów, próbujemy znaleźć „reguły”, których można by użyć do narysowania skojarzeń.

Zastosowanie

• Grupowanie jest często używane, gdy chcemy zidentyfikować klastry klientów o podobnych nawykach zakupowych, abyśmy mogli stworzyć określone strategie marketingowe skierowane do określonych klastrów
• Skojarzenie, najczęściej stosowane by opracować algorytm asocjacyjny, który mówi, że „jeśli klient kupi produkt X, jest wysoce prawdopodobne, że kupi również produkt Y” na podstawie zebranych danych „obserwacji” z koszyka zakupów.

Podsumowanie Algorytmów nadzorowanych vs nienadzorowanych

 

Uczenie wzmocnione Reinfoced Learning

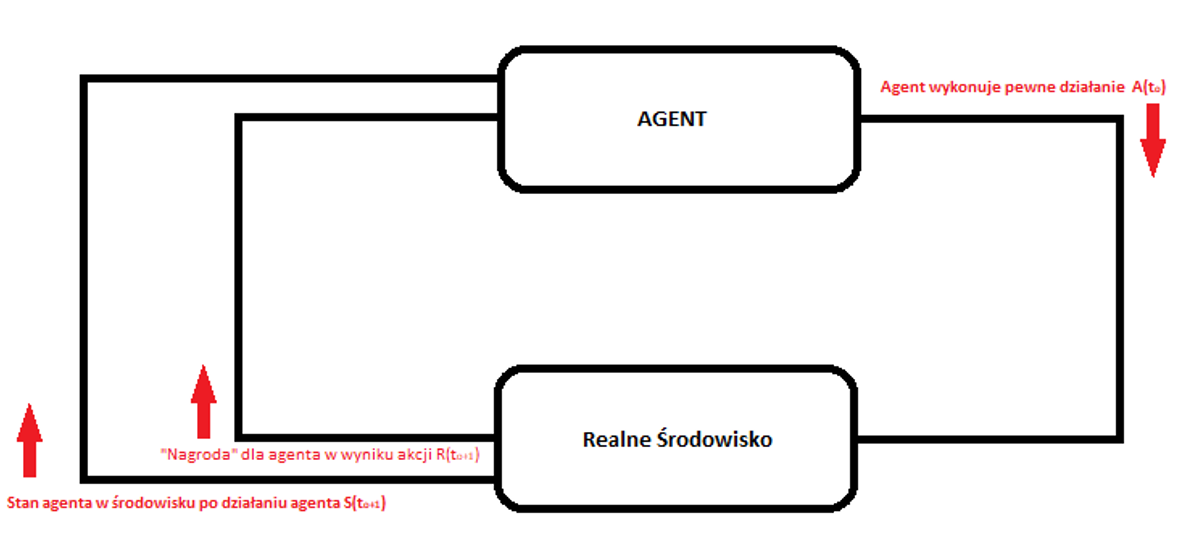
Uczenie się ze wzmocnieniem odnosi się do procesu uczenia się z zupełnie innego punktu widzenia. Wprowadza status agenta. Agent, którym może być robot, bot lub program komputerowy. Oprogramowanie oddziałuje na utworzone pliki i dynamiczne wprowadza dane o środowisku, w którym funkcjonuje do osiągnięcia określonego celu. Środowisko jest opisane za pomocą zestawu danych, w którym agent przyjmuje określone stany i w związku z tym agent może podejmować różne działania, aby przejść z jednego stanu do drugiego. Stany mogą przyjmować różne wartości np. stan celu, a jeśli agent osiągnie ten stan, otrzymuje dużą nagrodą jako wartość „true”. W innych stanach nagroda jest mniejsza np. „null”, nie istnieje, a nawet „false”. Celem uczenia się ze wzmocnieniem jest znalezienie optymalnej polityki lub funkcji mapowania, która określa działania, jakie należy podjąć w każdym ze stanów, bez nauczyciela, który wyraźnie powiedziałby, czy to prowadzi do stanu celu, czy nie.

Przykład: Labirynt. Możemy stosować wiele algorytmów do przeszukiwania labiryntu, ale nam chodzi o inna analizę. Potraktujmy naszego agenta jak żywą istotę, która szuka drogi do celu. Nasze zadanie to

1. Znaleźć cel w pierwszym kroku
2. Znaleźć najkrótszą drogę.

Mamy świadomość, że maszerując po labiryncie musimy przyjąć system oznaczania swoich dróg typu „tu byłem”, „poszedłem w ten korytarz”, „cofnąłem się tutaj i idę do innego korytarza” itd. W ten sposób wprowadzam do programu określone stany agenta a zapamiętuję je zapisując do pliku/plików. To nic innego jak algorytm uczący się który tworzy politykę, określa działanie, które ma być podejmowane w określonych konfiguracjach przeszukiwanych korytarzy. W końcu nasz agent znalazł cel i jest nagroda. Nasz algorytm zapamiętuje drogę, ale czy jest ona optymalna?  Niestety nasz agent będzie musiał powtórzyć przeszukiwanie z uwzględnieniem korytarzy, których jeszcze nie odwiedził, ponieważ być może jest inna krótsza droga. Odkrywane kolejne drogi wzmacniają nasze optimum. Na końcu naszych obliczeń zestawiamy wszystkie drogi i wyliczamy najkrótszą, nasz cel jest osiągnięty. Zapamiętując algorytm możemy wywołać dla niego najkrótszą drogę odwołując się do powiązanego z nim pliku, nasz agent już wie jak ma się zachować w przypadku tego labiryntu. (tej sytuacji/polityki, którą zastał).

Schemat obiegu danych dla Reinfoced Learning

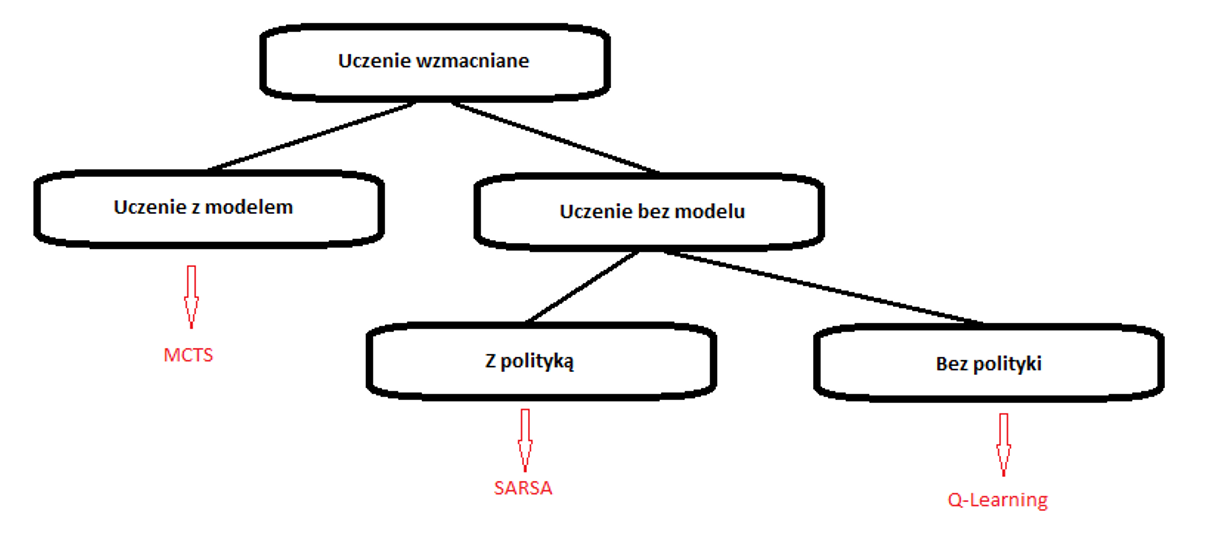
Wyróżniamy następujące główne typy uczenia Reinforced Learning

Grupa algorytmów wolnych od modeli:
Q-learning jest metodą spoza polityki, w której agent uczy się wartości na podstawie akcji pochodzącej z innej polityki,
SARSA jest metodą działającą w ramach polityki, w której agent uczy się wartości na podstawie bieżącego działania i wyprowadzonego od następnej polityki. Oznacza to że SARSA prowadzi pewna politykę kontroli własnych działań
Różnicę pomiędzy algorytmami najbardziej obrazowo wyjaśnia tzw. nauka chodzenia po klifie w taki sposób by z niego nie spaść. Problem omówiony jest szczegółowo tutaj https://studywolf.wordpress.com/2013/07/01/reinforcement-learning-sarsa-vs-q-learning

Grupa algorytmów bazujących na modelu. W tej grupie przedstawicielem wiodącym jest algorytm:
MCTS  (Monte Carlo Tree Search) –  jak sama nazwa wskazuje, to sposób na przeszukiwanie drzewa. Wewnątrz tego drzewa jego węzły reprezentują stany, a krawędź między węzłami reprezentuje wybór, którego podjąłby się przy przejściu z jednego stanu do drugiego. Algorytmy Monte Carlo to klasa algorytmów probabilistycznych. Oznacza to, że algorytm zwykle zwraca tylko przybliżenie rzeczywistego wyniku. Ale w kilku przypadkach udowodniono, że dąży do rzeczywistego wyniku, gdy ilość iteracji zmierza do nieskończoności.

Żeby zrozumieć sens drzewa Monte Carlo najłatwiej jest zacząć od zrozumienia analizy Monte Carlo. Samo podejście Monte Carlo jest szeroko stosowane w elektronice i wykorzystywane jest w analizie obniżenia kosztów produkcji. Najprościej przedstawić to na przykładzie dziury w płocie. Mamy czarny płot i dziurę w płocie, która ma nieznany kształt i na dodatek jest na czarnym tle. Z daleka nie widzimy ani dziury ani nie wiemy, gdzie ona jest.  Ale wymyśliliśmy, że postrzelamy sobie w ten płot karabinkiem do paintball np. z czerwoną farbą. Jeśli trafimy w płot to farba się rozleje. Jeśli trafimy w dziurę to kula z farba przeleci i nie pozostawi śladu. Oczywiście nasza farba do kontrast decyzyjny. Strzelając raz przy razie wykryjemy wszystkie dziury, a obstrzeliwując każdą z nich dowiemy się jakie mają kształty. Więcej informacji jest tutaj https://medium.com/@pedrohbtp/ai-monte-carlo-tree-search-mcts-49607046b204

Podstawowa mapa algorytmów klasy reinfoced learning.

Wstęp do metod Machine Learning podstawowe pojęcia

Normalizacja danych (zdemoralizowane SQL)

Techniki normalizacji danych dostosowują zbiór danych do formatu, którego algorytm uczenia maszynowego oczekuje jako dane wejściowe, a nawet mogą pomóc algorytmowi w szybszej nauce i osiągnięciu lepszej wydajności.

Wiele zestawów narzędzi do uczenia maszynowego automatycznie normalizuje i standaryzuje dane. Główne cele normalizacji to

• Organizacja danych tak, aby wyglądały podobnie we wszystkich rekordach i polach.
• Zwiększa spójność typów wejść, prowadząc do oczyszczania, generowania potencjalnych klientów, segmentacji i wyższej jakości danych.
• Eliminacja nieustrukturyzowanych danych i nadmiarowości (duplikatów) w celu zapewnienia logicznego przechowywania danych

Wyróżniamy następujące formy normalizacji.

1. 1NF

Najbardziej podstawową formą normalizacji danych jest 1NFm, która zapewnia brak powtarzających się wpisów w grupie. Aby każdy wpis został uznany za 1NF, musi mieć tylko jedną pojedynczą wartość dla każdej komórki, a każdy rekord musi być unikalny.

Przykład w omawianej wcześniej bazie danych wypożyczalni samochodów każdy klient musi mieć unikalny zestaw danych. Idealna krotka spełniająca ten wymóg to imię i nazwisko, adres, … i PESEL ten ostatni element jest absolutnie niepowtarzalny i w przypadku, kiedy przy normalizacji usuniemy IdKlienta (klucz) to dalej będzie to niepowtarzalny rekord.

2. 2NF

Aby być w regule 2NF, dane muszą najpierw dotyczyć wszystkich wymagań 1NF. Następnie dane muszą mieć tylko jeden klucz podstawowy. Aby oddzielić dane i mieć tylko jeden klucz podstawowy, wszystkie podzbiory danych, które można umieścić w wielu wierszach, należy umieścić w osobnych tabelach. Następnie można tworzyć relacje za pomocą nowych etykiet kluczy obcych.

Przykład w naszej bazie wypożyczalni samochodów główny klucz to Id Wypożyczenie (centrum gwiazdy). Do każdego wypożyczenia dodasz Klienta bez jego klucza co oznacza, że właśnie utworzono relację z obcym kluczem. W jednym rekordzie (krotce) umieszczono zestaw dwóch tabel bez konieczności zadawania rozbudowanego pytania SQL

3. 3NF

Aby dane znalazły się w regule 3NF, muszą najpierw spełniać wszystkie wymagania 2NF. Następnie dane w tabeli muszą być zależne tylko od klucza podstawowego. Jeśli klucz podstawowy zostanie zmieniony, wszystkie dane, na które ma to wpływ, należy umieścić w nowej tabeli.

Przykład nasza baza danych wypożyczalni wymaga konieczności pogrupowania ze względu np. na samochody spełniające normę poniżej Euro3 i powyżej Euro3 a jedyne czym dysponujemy to modele samochodów. W tym przypadku musimy zmienić nasz klucz podstawowy tj. Id Klient i utworzyć nowe tabele z podziałem, który nas interesuje do dalszych obliczeń.

Tak przygotowana baza danych może (a raczej powinna) podlegać kolejnym koniecznym modyfikacjom, które zostaną tutaj jedynie wymienione:

• Czyszczenie danych np. usuwanie danych powtarzających się – Data clearing
• Uzupełnianie wartości brakujących – Filling missing values
• Usuwanie wartości mocno odstających – ewidentne błędy przypadkowe – Remove outliers
• Dostosowanie danych – Data transformation
• Usuniecie zbędnych danych – Data reduction

Skalowanie, klasyfikacja danych

Załóżmy ze posiadamy dostęp do danych jak w zestawieniu poniżej

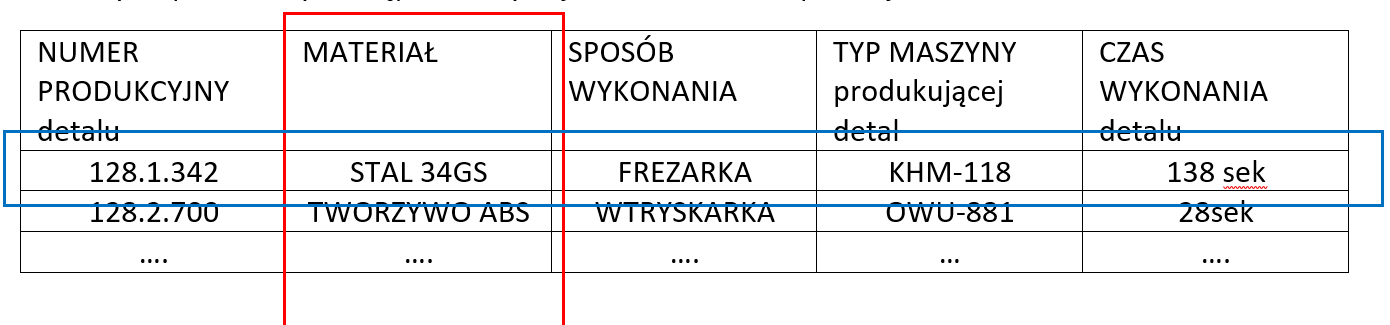
Nasz cel to stworzenie algorytmu, który zoptymalizuje produkcję wektory to nasze kolumny instancje/argumenty to wiersze.  Wywołując jeden z elementów argumentu mamy dostęp do wielu elementów z różnych kolumn. To oznacza, że możemy utworzyć wiele odwzorowań y=f(x) w zależności od tego jakimi zbiorami modeli chcemy dysponować.

To oznacza również, jak bardzo różnie możemy dobrać wartości atrybutów i jak różne zestawy zależności możemy uzyskać. Na przykład numer detalu to kombinacja liczbowa, maszyna to tekst, materiał to tekst i liczba lub kombinacje tych dwóch. Aby lepiej zrozumieć typy wartości, przyjrzyjmy się poniższym definicjom:

• Dane nominalne (jakościowe) – składają się z danych, które wzajemnie się wykluczają i nie są uporządkowane. Przykłady: kolor oczu, stan cywilny, rodzaj posiadanego samochodu itd. w naszym przykładzie to – sposób wykonania.
• Dane porządkowe – odpowiadają kategoriom, w których porządek ma znaczenie, ale nie różnica między wartościami, takimi jak poziom bólu, oceny z listów uczniów, ocena jakości obsługi, oceny filmów. Daną porządkową jest np. numer detalu w tabeli powyżej
• Dane interwałowe (przedziałowe , równomierne) – składają się z danych, w których różnica między dwiema wartościami osiąga wartości z przedziału, ale nie ma pojęcia miejsca pustego, na przykład standaryzowany wyniki egzaminu, temperatura w stopniach Fahrenheita lub jak w naszym przykładzie czas produkcji detalu. Czas produkcji za ten sam detal będzie oscylował wokół jakiejś średniej wytwarzania będzie zawsze większy od zera i osiągał wartość X, ale wykonanie detalu nie może być polem pustym.
• Dane współczynnika (współczynnikowe, ilorazowe) – mają wszystkie właściwości zmiennej interwałowej, a także jasną definicja odwzorowania, charakteryzuje się stałymi stosunkami i bezwzględnym zerem, np. gdy zmienna argumentu jest pusta, to zmienna funkcji będzie brakująca, ale znając model będzie możliwość odwzorowania na podstawie innych pełnych danych zestawu. Zmienne takie jak ceny akcji, tygodniowe wydatki na żywność są zmiennymi proporcjonalnymi.

Zatem skalowanie to w przypadku uczenia maszynowego to nie tylko efekt miary np. km/h, temperatura, ale także typ danej w kontekście składni i jej elementów cyfrowych i/lub tekstowych. Dla przejrzystości zagadnienia poniższe zestawienie ułatwia ocenę typu danej

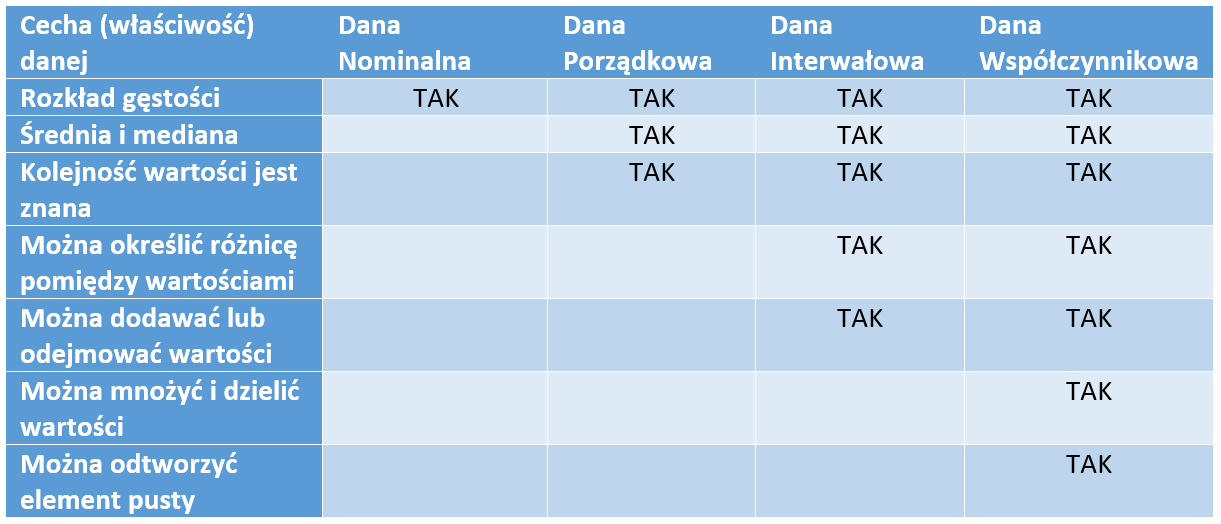
Przy czym dane nominalne i porządkowe odpowiadają wartościom dyskretnym, natomiast dane interwałowe (przedziału) i dane współczynnikowe mogą również odpowiadać wartościom ciągłym.

Należy przy tym zauważyć, że w uczeniu nadzorowanym skalowanie pomiaru i wartości atrybutów, które chcemy przewidzieć, dyktuje rodzaj algorytmu maszynowego, którego można użyć. Na przykład przewidywanie wartości dyskretnych z ograniczonego zbioru. Lista danych przyjmowana przez konkretny algorytm nazywana jest klasyfikacją i można ją uzyskać za pomocą drzew decyzyjnych, dla elementów dyskretnych, natomiast dla przewidywania wartości ciągłych (np. skala temperatury) nazywane są regresją, którą można osiągnąć za pomocą drzew modelowych lub modeli.

Zestaw (zbiór) danych

Skategoryzowanie danych to tylko krok w eksploracji danych. Następnym krokiem, zagadnieniem jest sprawdzenie, skąd pochodzą dane. Gromadzone dane mogą być bardzo niezorganizowane i w bardzo różnych formatach, co jest typowym wynikiem odczytu (zrzutu)  z bazy/baz/tabel danych, Internetu, systemu plików lub innych dokumentów. Większość narzędzi do uczenia maszynowego wymaga prezentacji danych w określonym formacie w celu wygenerowania właściwego wyniku. Mamy dwie możliwości: obserwować dane z istniejących źródeł lub generować dane za pomocą ankiet, symulacji i eksperymentów. Każda z tych metod ma za zadanie zebranie i sformatowanie właściwych danych do właściwego algorytmu.

Wyszukiwanie i/lub obserwacja danych

Jak wspomniano wcześnie głównym źródłem to strony WWW i dostęp do danych jak danych GUS jak zbiory danych treningowych dostępnych poprzez Internet W tym przypadku najistotniejsza jest ich wiarygodność Główną wadą gromadzonych danych jest to, że gromadzenie ich wymaga czasu i przestrzeni. Ponadto te dane obejmują tylko to, co się wydarzyło; na przykład intencje i wewnętrzne i zewnętrzne motywacje nie są gromadzone. Wreszcie takie dane mogą być zaszumione, niekompletne, niespójne, a nawet może się z czasem zmienić. Inną opcją jest zbieranie pomiarów z czujników takich jak bezwładnościowe i lokalizacyjne, czujniki w urządzeniach mobilnych, czujniki środowiskowe i klucz do monitorowania agentów oprogramowania wskaźniki efektywności. Ten typ danych to są najcenniejsze zbiory. Dane ruchowe operatorów, dane środowiskowe, które wraz z połączeniem z bazami danych zakładów przemysłowych umożliwiają wykrycie niezliczonej ilości korelacji i zastosowań ML oraz AI.

Tworzenie własnych zbiorów danych

Alternatywnym podejściem jest wygenerowanie danych, na przykład za pomocą ankiety. W projektowaniu ankiet musimy zwrócić uwagę na próbkowanie danych; czyli kim są respondenci biorący udział w ankiecie. Pozyskujemy dane tylko od tych respondentów, którzy są dostępni i chętni do odpowiedzi. Respondenci mogą również udzielić odpowiedzi, które są zgodne z ich obrazem siebie i oczekiwaniami badacza.

Alternatywnie dane mogą być zbierane za pomocą symulacji, w których ekspert dziedzinowy określa model zachowania użytkowników na poziomie mikro. Na przykład symulacja tłumu wymaga określenia, jak różne typy użytkowników będą się zachowywać w tłumie. Niektóre przykłady to podążanie za tłumem, szukanie ucieczki i tak dalej. Symulację można następnie przeprowadzić w różnych warunkach, aby zobaczyć, co się stanie. Symulacje są odpowiednie do badania zjawisk makro i zachowań emergentnych, jednak zazwyczaj trudno je zweryfikować empirycznie. Co więcej, mozna projektować eksperymenty, aby dokładnie objąć wszystkie możliwe wyniki, w których wszystkie zmienne są stałe i manipulować tylko jedną zmienną na raz. Jest to najbardziej kosztowne podejście, ale zazwyczaj zapewnia najlepszą jakość.

Uzupełnianie brakujących wartości

Algorytmy uczenia maszynowego generalnie nie działają dobrze z brakującymi wartościami. Rzadko spotykanymi wyjątkami są drzewa decyzyjne, klasyfikator Naive Bayes i niektóre algorytmy uczące się na podstawie reguł. To jest bardzo ważne, aby zrozumieć i przeanalizować zbiór pod katem pustych pól, dlaczego brakuje wartości. Może brakować z powodu wielu przyczyn, takie jak błąd przypadkowy, błąd systematyczny i szum czujnika. Najważniejsze jest by umieć zidentyfikować w zbiorze brakujące dane. Istnieje wiele sposobów radzenia sobie z brakującymi wartościami, jak pokazano w poniższej liście.

• Usunięcie instancji – jeśli jest wystarczająco dużo danych i tylko kilka nieistotnych braków To w przypadku wystąpienia niektórych braków danych można bezpiecznie usunąć te wystąpienia.
• Usunięcie atrybutu – usunięcie atrybutu ma sens, gdy większość brakujących wartości to wartości stałe lub atrybut jest silnie skorelowany z kolejnym atrybutem.
• Przypisanie specjalnej wartości – może się zdarzyć, że brakuje wartości z ważnych powodów, np. wartość jest poza zakresem, wartość atrybutu dyskretnego nie jest zdefiniowana oraz gdy wartość jest niemożliwa do uzyskania lub zmierzenia. Na przykład, jeśli dana osoba nigdy nie oceniła filmu lub jego ocena w tym filmie nie istnieje.
• Wyznaczenie średniej wartości atrybutu – jeśli mamy ograniczoną liczbę wystąpień, a każde usunięcie instancji lub atrybutów stanowi poważne zubożenie zbioru to w takim przypadku możemy oszacować brakujące wartości, przypisując średnią wartość atrybutu.
• Prognozowanie wartość z na postawie innych atrybutów – można próbować przewidywać wartość na podstawie poprzednich wpisów, jeśli atrybut posiada zależności zbieżne korelacyjne

Wartości może brakować z wielu powodów, dlatego ważne jest, aby zrozumieć, dlaczego brakuje wartości, i jaki jest powód, że jest ona nieobecna lub uszkodzona.

Czyszczenie danych

Czyszczenie danych, znane również jako szorowanie danych, to proces składający się z następujących kroków:

1. Identyfikacja niedokładnych, niekompletnych, nieistotnych lub uszkodzonych danych w celu usunięcia ich z dalszego przetwarzania
2. Parsowanie danych (składanie w określone zbiory) poprzez wydobywanie interesujących informacji lub sprawdzanie, czy ciąg danych ma akceptowalny format
3. Przekształcenie danych do wspólnego formatu kodowania, na przykład UTF-8 lub int32, skali czasu lub znormalizowanego zakresu
4. Przekształcenie danych we wspólny schemat danych; na przykład, jeśli zbieramy pomiary temperatury z różnych typów czujników, możemy chcieć, aby miały taką samą strukturę np. taki sam element sondy pomiarowej przykładowo tylko sonda PT100 a nie np. Pt100 i Pt 1000.

Usuwanie wartości odstających

Wartości odstające w danych to wartości, które różnią się od innych wartości w serii i wpływają w dużym stopniu na wszystkie metody uczenia się. Mogą to być wartości ekstremalne, które można wykryć za pomocą przedziałów ufności i usunąć za pomocą progu. Najlepszym podejściem jest wizualizacja danych i sprawdzenie wizualizacji w celu wykrycia nieprawidłowości. Dlaczego to takie istotne? Załóżmy, że obrabiarka frezuje dany element w określonym czasie jednakże w trakcie zbierania pomiarów uszkodzeniu uległ frez w wyniku czego dany element został wykonany (nie istotne czy źle czy dobrze) w innym niż typowy czas. Użycie tego zbioru jako danych treningowych bez wyłapania anomalii będzie stanowić poważny błąd. Taki element należy wykluczyć ponieważ może mieć wpływ na wyłapanie anomalii w przyszłości.

Transformacja (dostosowywanie) danych

Techniki transformacji danych dostosowują zbiór danych do formatu, który jest używany przez uczenie maszynowe. Algorytm oczekuje jako danych wejściowych takich danych które jest w stanie samodzielnie przetwarzać. Jest to szczególnie istotne w przypadku algorytmów zastosowanych do działań w czasie rzeczywistym, gdzie np. algorytm predykcji ma służyć w podejmowaniu decyzji dla regulacji automatyki sterującej. Nazywa się to również przetwarzaniem danych lub przepychaniem danych.

Transformacja poosiowa (przesuwanie danych po osi lub wektorze)

Najbardziej znana jest standaryzacja rozkładu Gaussa, która zakłada, że w celu wykonania stosownych obliczeń sprowadzamy dowolny rozkład normalny do rozkładu standaryzowanego w taki sposób, aby średnia wartość wynosiła µ=0, a odchylenie σ=1. Transformacje wykonujemy z zastosowaniem poniższej zależności.

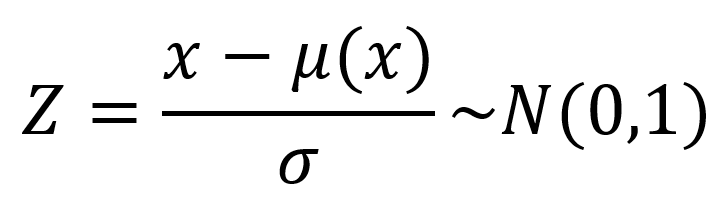
gdzie     μ- średnia rozkładu

                ϭ-odchylenie standardowe

Wiele zestawów narzędzi do uczenia maszynowego automatycznie normalizuje i standaryzuje dane.

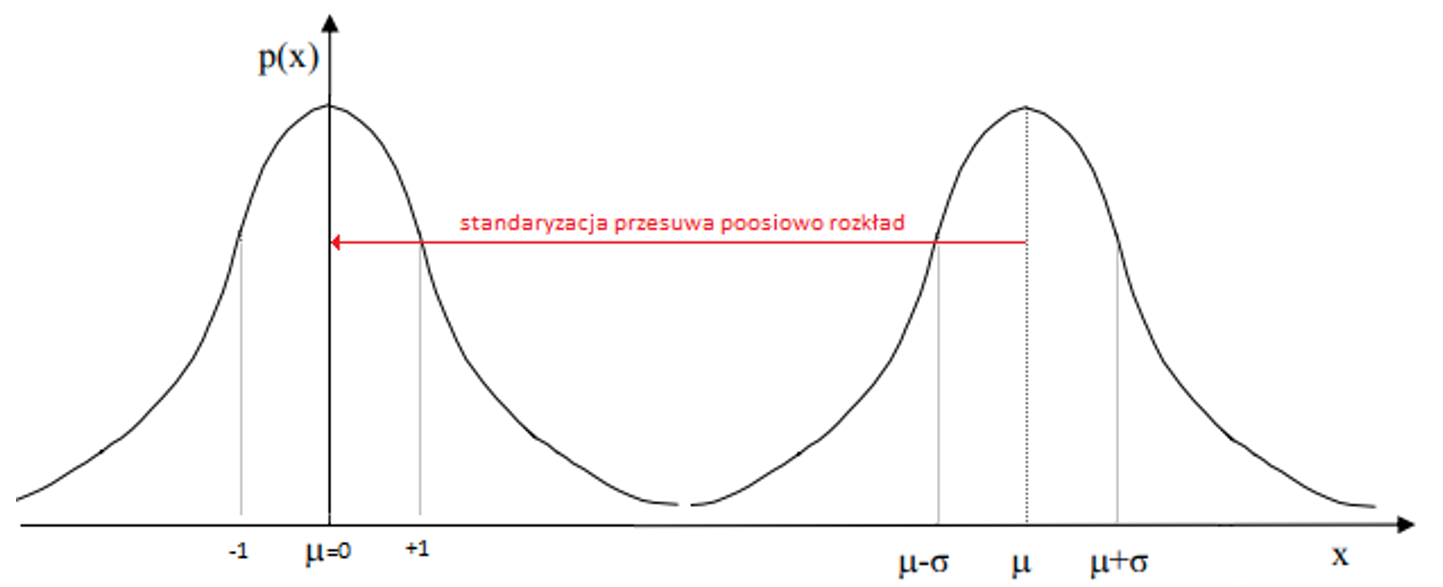
Przykład obliczeń: mamy rozkład gdzie μ=7 a ϭ=6 → N(7,6). Znaleźć zmienną „Z” dla rozkładu standaryzowanego przy danym X=4 → Z=(4-7)/6=-1/3 ~ N(0,1).

Dyskretyzacja

Ostatnią omawiana techniką transformacji jest dyskretyzacja, która dzieli zakres ciągłego atrybutu na przedziały. Dlaczego powinniśmy się tym przejmować? Niektóre algorytmy, takie jak drzewa decyzyjne i Naive Bayes preferują atrybuty dyskretne.

Najczęstsze sposoby wyboru interwałów (przedziałów) są następujące:

• Równa szerokość – przedział zmiennych ciągłych jest podzielony na k przedziałów o równej szerokości
• Równa częstotliwość – przypuśćmy, że istnieje N instancji, każdy z k przedziałów zawiera w przybliżeniu N lub k instancji
• Minimalna entropia – to podejście rekurencyjnie dzieli interwały, aż entropia, która mierzy nieuporządkowanie, zmniejszy się bardziej niż wzrost entropii wprowadzony przez podział interwałowy.

Dwie pierwsze metody wymagają od nas określenia liczby interwałów, podczas gdy ostatnia metoda automatycznie ustawia liczbę interwałów; wymaga jednak zmiennej klas, co oznacza, że ​​nie będzie działać w przypadku nienadzorowanych zadań uczenia maszynowego.

Redukcja danych

Redukcja danych dotyczy wielu atrybutów i instancji. Liczba atrybutów odpowiada liczbie wymiarów w naszym zbiorze danych. Wymiary o niskiej mocy predykcyjnej mają bardzo mały wkład w ogólny model i powodują wiele szkód. Na przykład atrybut o losowych wartościach może wprowadzać pewne losowe wzorce, które zostaną odebrane przez algorytm uczenia maszynowego. Może się zdarzyć, że dane zawierają dużą liczbę braków danych, przy czym musimy znaleźć przyczynę braków w dużej liczbie i na tej podstawie może je wypełnić jakąś alternatywną wartością lub imputować lub całkowicie usunąć atrybut. Jeśli brakuje 40% lub więcej wartości, może być wskazane usunięcie takich atrybutów, ponieważ wpłynie to na wydajność modelu.

Drugim czynnikiem jest wariancja, gdzie zmienna stała może mieć niską wariancję, co oznacza, że ​​dane są bardzo blisko siebie lub nie ma dużej zmienności w danych. Aby poradzić sobie z tym problemem, pierwszy zestaw technik usuwa takie atrybuty i wybiera te najbardziej obiecujące. Proces ten jest znany jako selekcja cech lub selekcji atrybutów i obejmuje metody takie jak ReliefF, zysk informacji i indeks Giniego. Metody te koncentrują się głównie na atrybutach dyskretnych. Inny zestaw narzędzi, skoncentrowany na ciągłych atrybutach, przekształca zbiór danych z oryginalnych wymiarów do przestrzeni o niższych wymiarach. Na przykład, jeśli mamy zbiór punktów w przestrzeni trójwymiarowej, możemy wykonać rzut na przestrzeń dwuwymiarową. Część informacji jest tracona, ale w sytuacji, gdy trzeci wymiar jest nieistotny, my nie tracimy

dużo, ponieważ struktura danych i relacje są prawie doskonale zachowane. Można to wykonać następującymi metodami:

• Rozkład według wartości osobliwych (SVD)
• Analiza głównych składników (PCA)
• Eliminacja funkcji wstecz/do przodu
• Analiza czynników
• Liniowa analiza dyskryminacyjna (LDA)
• Autokodery sieci neuronowych

Kolejny problem związany z redukcją danych jest uzależnienie od zbyt dużej liczby przypadków. Na przykład mogą być duplikatami lub pochodzić z bardzo gęstego strumienia danych. Główną ideą jest wybranie podzbioru instancji w taki sposób, aby dystrybucja wybranych danych nadal przypominała pierwotną dystrybucję danych, a co ważniejsze, obserwowany proces. Techniki mające na celu zmniejszenie liczby wystąpień obejmują losowe próbkowanie danych, stratyfikację i inne. Po przygotowaniu danych możemy przystąpić do analizy i modelowania danych.

Klasyfikacja

Najprościej o klasyfikacji możemy powiedzieć jako o technice określania, do której klasy należy jednostka zależna, na podstawie co najmniej jednej zmiennej niezależnej. Ilustruje to poniższy rysunek.

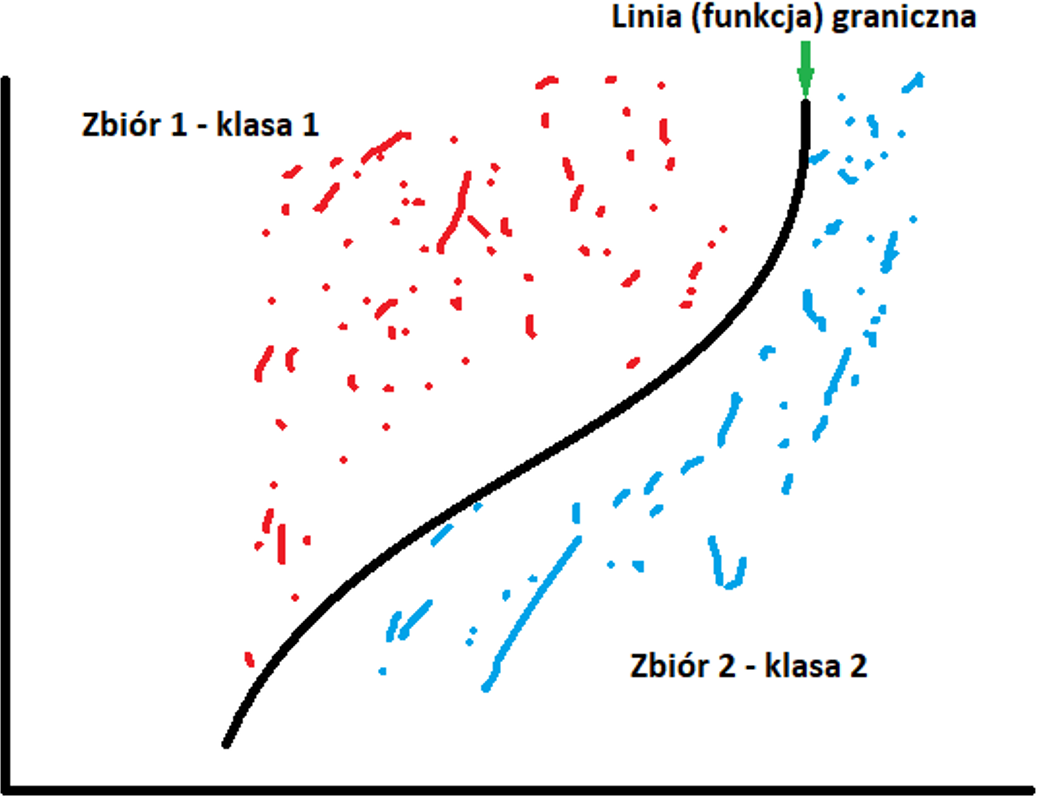
Klasyfikację można zastosować, gdy mamy do czynienia z klasą dyskretną, której celem jest przewidzenie jednej z wzajemnie wykluczających się wartości w zmiennej docelowej. Przykładem może być ocena kredytowa, gdzie ostateczną prognozą jest to, czy danej osobie można udzielić  kredyt, czy nie. Do najpopularniejszych algorytmów klasyfikujących należą drzewa decyzyjne, klasyfikatory Naive Bayes, maszyny SVM, sieci neuronowe czy uczenie zespolone.

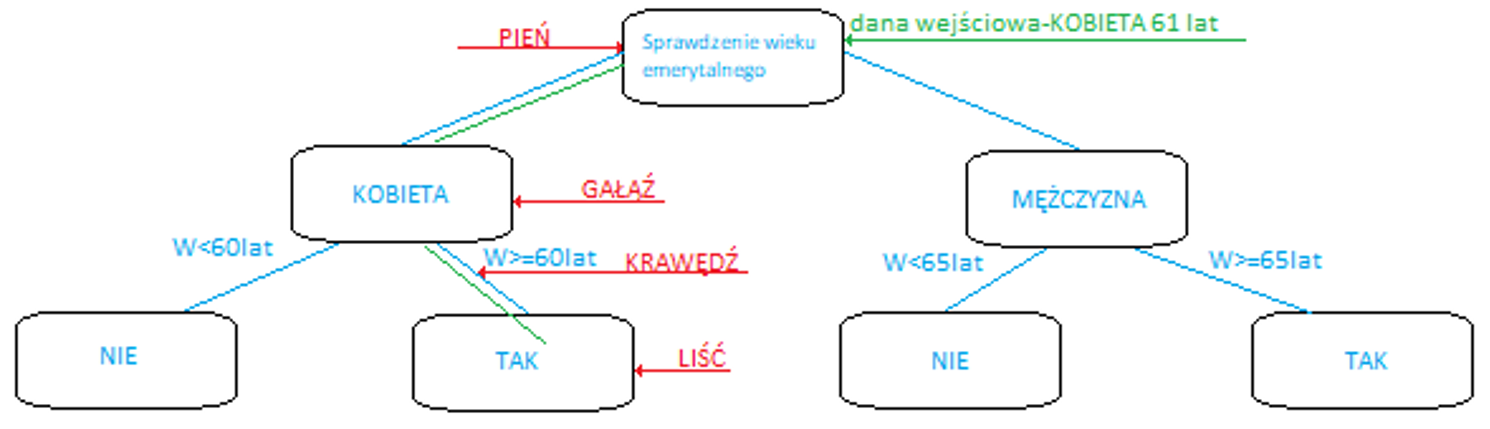
Drzewa decyzyjne

Metoda drzewa decyzyjnego to koncepcja tworzy drzewo klasyfikacyjne, w którym każdy węzeł odpowiada jednemu z atrybutów, krawędzie odpowiadają możliwej wartości (lub przedziałom) atrybutu, z którego pochodzi węzeł; a każdy liść odpowiada etykiecie klasy i stanowi wynik decyzji. Drzewo decyzyjne może służyć do wizualnego i jawnego reprezentowania modelu predykcyjnego, co czyni go bardzo przejrzystym klasyfikatorem. Godne uwagi algorytmy to ID3 i C4.5, chociaż istnieje wiele alternatywnych implementacji i ulepszeń (na przykład J48 w Weka).

Przykład graficzny prostego drzewa decyzyjnego czy badana osoba nabyła prawa emerytalne. Dane wejściowe „płeć”; „wiek”

Klasyfikatory proabilistyczne

O klasyfikatorze probabilistycznym mówimy wtedy, kiedy mając zestaw wartości atrybutów, klasyfikator probabilistyczny jest w stanie przewidzieć rozkład w zestawie klas, a nie w dokładnej klasie. Klasyfikacja probabilistyczna oznacza, że model użyty do klasyfikacji jest modelem probabilistycznym, w szczególności modele te mogą podawać prawdopodobieństwo wystąpienia instancji należącej do klasy pozytywnej lub negatywnej. Następnie do nas należy decyzja, czy instancja jest dodatnia, czy ujemna na podstawie prawdopodobieństw podanych przez model. Dwie powszechnie stosowane formy modeli probabilistycznych to:

• Modele generatywne: Jeśli x oznacza instancję (argument), a y oznacza etykietę, to w modelach generatywnych uczymy się łącznego rozkładu względem x i y, P(x, y) lub równoważnie P(x|y) i P(y). Rozpoczyna się od założenia rozkładu parametrycznego dla P(x, y) (lub P(x|y) i P(y)) a następnie uczenia parametrów przy użyciu danych uczących. Modele te nazywane są generatywnymi, ponieważ po poznaniu parametrów modele te pozwalają nam „generować” z nich nowe punkty danych poprzez próbkowanie. Przykładem takiego modelu klasyfikacji jest Naive Bayes.
• Modele dyskryminacyjne: Jeśli x oznacza instancję (argument), a y oznacza etykietę, to w modelach dyskryminacyjnych uczymy się warunkowego rozkładu na y przy danym x, P(y|x). Rozpoczyna się od założenia rozkładu parametrycznego dla P(y|x), a następnie uczenia parametrów przy użyciu danych uczących. Modele te nazywane są rozróżniającymi, ponieważ po poznaniu parametrów modele te pozwalają nam jedynie „rozróżniać” klasy dla danej instancji na podstawie prawdopodobieństw, które zapewniają. Modele te nie umożliwiają generowania nowych punktów danych, takich jak modele generatywne. Przykładem takiego modelu klasyfikacji jest regresja logistyczna.

Metoda Kernel (metoda/funkcja jądra) i SVM

Każdy model liniowy można przekształcić w model nieliniowy, stosując manipulację jądra do modelu — zastępując jego cechy (predyktory) funkcją jądra. Innymi słowy, jądro pośrednio przekształca nasz zbiór danych w wyższe wymiary. Sztuczka z jądrem wykorzystuje fakt, że często łatwiej jest rozdzielić instancje w większej liczbie wymiarów. Funkcje jądra umożliwiają manipulowanie danymi jak by był rzutowany w przestrzeń wyższego wymiaru, operując na nim w jego pierwotnej przestrzeni. Żeby zrozumieć zagadnienia kernelowske trzeba najpierw omówić zagadnienie związane z pojęciem Support Vector Machine (SVM).

SVM to nadzorowane modele uczenia maszynowego które analizują dane w celu ich klasyfikacji (tutaj klasyfikację należy rozumieć pod kątem tego – „co należy do czego”). Jeśli spojrzymy na drzewo opisane w „Drzewa decyzyjne” to kobieta lat 61 jest sklasyfikowana jako emeryt. Jest to klasyfikacja niejako ustawiona „na sztywno”, inaczej będzie to wyglądało w przypadku klasyfikacji SVM. Dla zbiorów danych SVM to klasyfikator formalnie zdefiniowany jako rozdzielająca hiperpłaszczyzna. Hiperpłaszczyzna to podprzestrzeń o jeden wymiar mniej niż jej przestrzeń otoczenia, czyli przestrzeni, w której znajdują się badane zbiory. Jest klasyfikatorem, który reprezentuje dane uczące jako punkty w przestrzeni podzielone na kategorie przerwą jak najszerszą. Nowe punkty są następnie dodawane do przestrzeni poprzez przewidywanie, do której kategorii należą i do jakiej przestrzeni będą należeć.

Przykład: Podzieliśmy owoce z koszyka na dwie grupy – waga, kształt. Powiedzmy, że robiły to osoby z zawiązanymi oczami. Wyszły nam dwie grupy owoców i nie było to trudne do podziału, ponieważ, w koszyku były śliwki węgierki i gruszki klapsy.

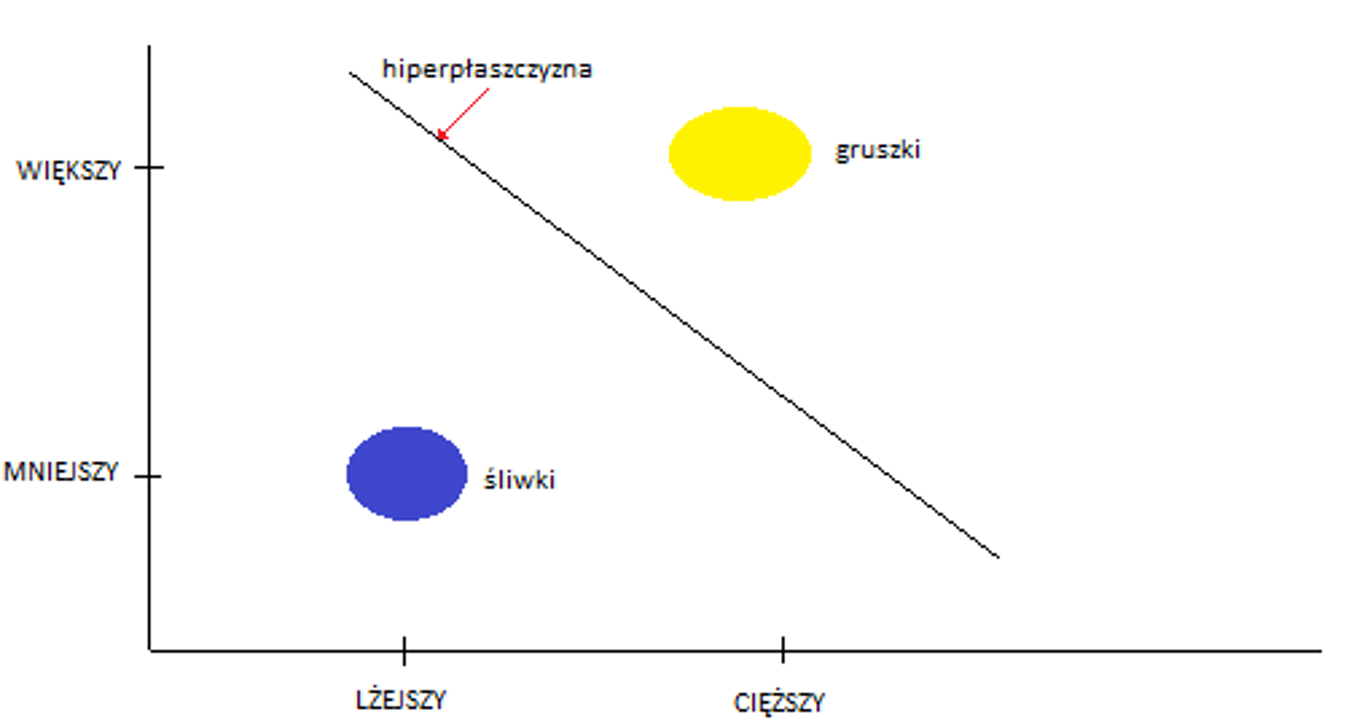
Matematycznie miejsce w przestrzeni dwuwymiarowej (lub obiekt/klasa w przestrzeni) jest nieformalnie zdefiniowany jako element o współrzędnych (x, y, na osiach rzędnej i odciętej) i są to dane potrzebne do określenia dowolnego punktu (jak np. mniejszy i lżejszy oraz większy i cięższy) w tej przestrzeni. Rzeczywista przestrzeń otoczenia takiego obiektu różni się od przestrzeni matematycznej otaczającej obiekt matematyczny. Matematyczny obiekt jest abstrakcyjny i wynikający z matematyki opis też jest abstrakcyjny dla obiektu/rzeczy, który nie istnieje w danym czasie i miejscu rzeczywistym, ale raczej istnieje jako rodzaj idei lub abstrakcji. W omawianym przykładzie mówimy, że centroidy zbiorów i same zbiory są mocno skorelowane ze swoimi klasami, oraz, że nie występują elementy niejednoznaczne tj. takie które teoretycznie mogą należeć zarówno do jednego lub drugiego ze zbiorów. Dlaczego to takie istotne? Ponieważ dla SVM w takim przypadku hiperpłaszczyzna dla przestrzeni dwuwymiarowej jest jednowymiarową linią prostą oddzielającą te dwa zbiory z odpowiednim marginesem (z założenia jak najszerszym).

Inaczej mówiąc kwalifikacja zbioru (matematycznie) ulega znaczącemu uproszczeniu. Nie mamy przestrzeni dwóch zbiorów śliwka=f(x_1, y₁) oraz gruszka=f(x_2, y₂), ale prosty zapis rozdziału dwóch klas oddzielonych od siebie równaniem y=ax+b (równanie prostej na płaszczyźnie dwuwymiarowej) i pasa marginesu. Po fazie trenowania i przejściu do fazy testu, oznacza to uproszczenie kwalifikacji na podstawie tylko jednej danej(zmiennej) bo albo coś znajduje się z prawej strony nowej osi podziału albo z jej lewej strony lub albo nad nią, albo pod nią w zależności jak na to patrzymy. Na co powinniśmy jednak zwrócić szczególną uwagę to fakt, że w tym przypadku mamy brak losowości. Nawet z zawiązanymi oczami po prostu bardzo trudno o jakikolwiek błąd. Trzymając w ręku jeden wzorzec biorąc w drugą czy to śliwkę czy gruszkę bez problemu odróżnimy te dwa owoce. SVM uprościło nam proces decyzji. Bardziej szczegółowe wyjaśnienie opisano tutaj https://www.slideshare.net/saipuji1/support-vector-machine-and-implementation-using-weka

Powróćmy zatem do kwestii kernel czyli jądra. Rozważmy inną kwestie koszyka z owocami. Tym razem w koszyku są dwa gatunki jabłek. Niech będą to np. Ligol i Lobo. Te pierwsze powszechnie rozpoznawalne po dużej wielkości te drugie rozpoznawalne jako lekko stożkowate. W tym przypadku podział z zawiązanymi oczami nie jest taki oczywisty. Dlaczego? Ponieważ nasza rozróżnialność będzie obarczona dużym błędem a zbiory będą się wzajemnie przenikać. Nie znając bardziej szczegółowych cech każdy z tych owoców każde będzie dla nas po prostu jabłkiem. Przekształcany nasz zbór dwuwymiarowy do zbioru trójwymiarowego dodając nową cechę „kształt”  jak poniżej

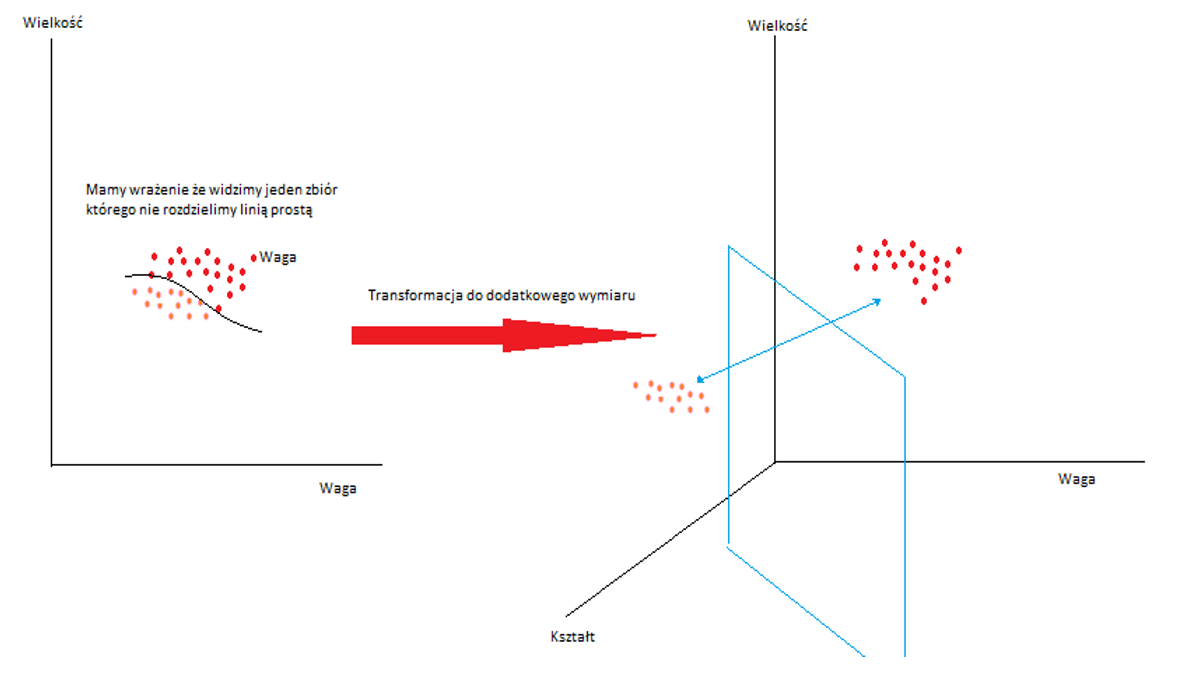
Widzimy, że zbiór widoczny od strony płaszczyzny jest dalej dwuwymiarowy, ale od strony nowej przestrzeni trójwymiarowej jest widoczna różnica zbiory są bardziej rozdzielne. Z definicji sztuczka kernel (kernel trick) jest opisana

K(x, y)=<f(x), f(y)>

gdzie     K-funkcja Kernel od wskazanych zmiennych x, y w przestrzeni n wymiarowej

                f-funkcje od x, y w przestrzeni m wymiarowej takiej, że m>n

W przypadku normalnych obliczeń, każda ze współrzędnych wymaga najpierw obliczeń funkcji f(x) oraz F(y) w nowej przestrzeni a następnie przemnożenie skalarnie (iloczyn skalarny) elementów w nowej przestrzeni. Otrzymany wynik jest skalarem co w praktyce oznacza, że do określenia poprawnego wyniku musimy powrócić do pierwotnej przestrzeni.

Jak to wygląda matematycznie – przykład bez kernel:

Mamy zbiór elementów X=(x1, x2) oraz elementów Y=(y1, y2), nowe funkcje będą zatem miały postać f(x)=(x1x1, x1x2, x2x1, x2x2) oraz f(y)-(y1y1, y1y2, y2y1, y2y2) czyli z dwóch mamy 4 wymiary. Liczbowo – niech x=(1, 2)  oraz y=(4,5) będzie to odpowiednio
f(x)=(1, 2, 2, 4) oraz f(y)=(16, 20, 20, 25) zatem <f(x), f(y))>=(1*16+2*20+2*20+4*25)=196

Te same obliczenia w kernelem natomiast będą następujące:
K(x, y)=(<x, y>)²  podstawiając te same dane dla x oraz y mamy odpowiednio (1*4+2*5)^2=14²=196

Podsumowując kernelem zwiększając przestrzeń o jeden raz więcej osiągamy ten sam wynik przy znacznie mniejszej ilości działań. Szczegóły na stronie https://www.quora.com/What-are-kernels-in-machine-learning-and-SVM-and-why-do-we-need-them/answer/Lili-Jiang?srid=oOgT

Sztuczne sieci neuronowe

Sztuczne sieci neuronowe są inspirowane strukturą biologicznych sieci neuronowych i są zdolne do uczenia maszynowego, a także rozpoznawania wzorców. Są powszechnie używane zarówno dla problemów regresji, jak i klasyfikacji, obejmujących szeroką gamę algorytmów i wariacje dla wszystkich rodzajów problemów. Niektóre popularne metody klasyfikacji to perceptron, ograniczona maszyna Boltzmanna (RBM) czy głębokie sieci neuronowe.

Metody zespołowe

Metody zespołowe składają się z zestawu różnych słabszych modeli w celu uzyskania lepszej wydajności predykcyjnej. Poszczególne modele są trenowane oddzielnie, a ich predykcje są następnie łączone w pewien sposób w celu uzyskania ogólnej prognozy. W związku z tym zestawy zawierają wiele sposobów modelowania danych, co powinno z założenia prowadzić do lepszych wyników. Jest to bardzo potężna klasa technik i jako taka jest bardzo popularna. Ta klasa obejmuje boosting, bagging, AdaBoost i losowy las. Główne różnice między nimi to rodzaj słabych uczniów, których należy łączyć, oraz sposoby ich łączenia.

Metody oceniania klasyfikacyjne

W klasyfikacjach liczymy, ile razy klasyfikujemy coś na TAK lub NIE by dojść do celu i ostatecznej odpowiedzi jak dokładnie to zrobiliśmy. Dobrym przykładem jest np. gra w odgadywanie jaki mam zawód gdzie osoba pytająca dostaje tylko odpowiedź TAK lub NIE. Ostatecznie może udać się nam odgadnąć zwód prawidłowo, lub znacząco przybliżyć się do wiedzy co to za praca, albo się dowiedzieć  że to osoba nie pracuje.

Klasyfikacja binarna

W metodach oceny klasyfikacji ten system jest nieco bardziej rozbudowany. Załóżmy, że istnieją dwie możliwe etykiety klasyfikacyjne: tak i nie w systemie gdzie porównujemy wartość prognozowaną z wartością otrzymaną w rzeczywistości.  W odpowiedzi mamy cztery możliwe wyniki oceny, jak pokazano w poniższej tabeli czasami nazywanej macierzą błędów:

Stany zaznaczone na zielono zaliczamy do wyników właściwych pozostałe to fałszywe alarmy (chybienia).  Podsumowując wyniki z tabeli otrzymujemy dwie podstawowe miary klasyfikacji:

• Błąd klasyfikacji
• Dokładność klasyfikacji

Błąd klasyfikacji (classification error) określa zależność

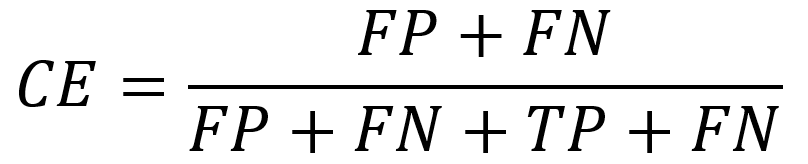
Trafność klasyfikowania (classification accuracy) określa zależność

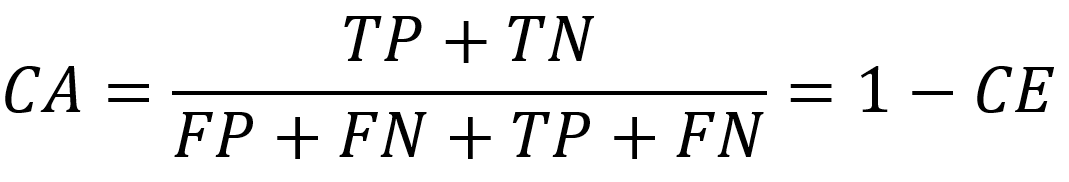
Od podanej powyżej stosowanej zasady oceny istnieje wyjątek. Są to tzw. klasy niezrównoważone. Dotyczy to zadań w których liczba przypadków jest nierównomiernie rozłożona. Przykładem jest klasyfikowanie, czy transakcja kartą kredytową jest nadużyciem, czy nie, gdzie statystycznie jest 99,99% normalnych transakcji i tylko niewielki procent nadużyć. Klasyfikator, który mówi, że każda transakcja jest normalna, ma 99,99% trafności, ale nas interesują przede wszystkim te nieliczne klasyfikacje, które zdarzają się bardzo rzadko. Tego typu zagadnienia rozwiązuje się albo poprzez przebudowę algorytmów, albo bardziej powszechnie stosowane rozwiązanie – poprzez zmianę podejścia do próbkowania danych.

W ramach klasyfikacji binarnej dodatkowo stosuje się oceny

• Precyzja (precision) – proporcja elementów prawidłowo uznanych za pozytywne PP(ang. TP) do wszystkich elementów rzeczywiście pozytywnych

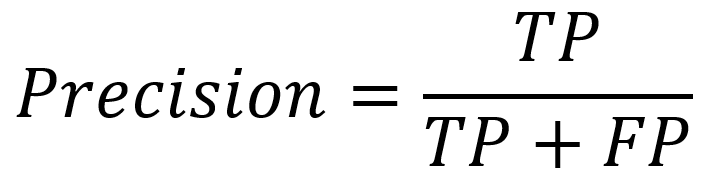
• Czułość (recall)- proporcja elementów prawidłowo uznanych za pozytywne PP (ang. TP) do sumy elementów prawidłowo i błędnie uznanych za pozytywne.

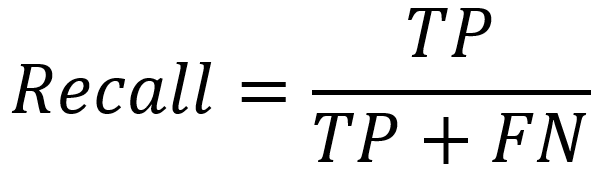
• Specyficzność FPR False Positive Rate określana wzorem:

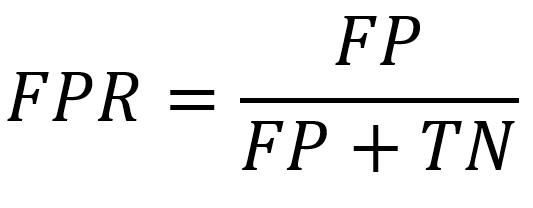
Powszechne jest łączenie tych dwóch pierwszych powyższych parametrów (Precision, Recall) i raportowanie miary F, która uwzględnia zarówno precyzję, jak i czułość, aby obliczyć wynik jako średnią ważoną, gdzie wynik osiąga najlepszą wartość przy 1, a najgorszą przy 0, w następujący sposób:

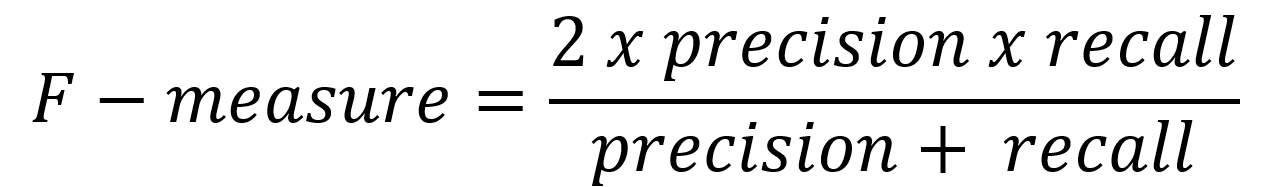
Ani sama precyzja, ani czułość nie opowiadają całej historii zdarzeń. Miara F odwołuje się do trzech danych – liczebność próby, liczby klas oraz środek klasy.

Po obliczeniu precyzji i czułości dla problemu klasyfikacji binarnej, oba wyniki można połączyć w obliczeniach F-Measure w jeden miarodajny wynik łączący wiele danych cząstkowych.

Przykład. Scenariusz – mamy linię produkcyjną sortowania jabłek której zadaniem jest oddzielenie jednego konkretnego gatunku „X” od jabłek innych gatunków. Załóżmy że nasza linia sortująca mierzy pewne parametry z maszyn na taśmie które są podłączone do naszej sztucznej inteligencji, a oczekiwana skuteczność sortowania ma być na poziomie F-measure na poziomie 0,95 (95%). Przykładowo są to następujące parametry:

1. waga jabłka
2. barwa jabłka
3. kształt jabłka

Łatwo zauważyć że niektóre parametry wymuszają ocenę obrazu jabłka (dużo danych wzorców w pamięci) w związku z tym cały system poddaliśmy procesowi Machine Learning. Podczas uruchomienia próbnego partii 1000 jabłek otrzymaliśmy następującą macierz wyników sortowania maszynowego i pomiarów ręcznych laboratoryjnych tej samej partii (zakładamy że błąd pomiaru laboratoryjnego wynosi 0)

czyli

1. 700 jabłek gatunku „X” rozpoznano i przesortowano prawidłowo,
2. 250 jabłek innych gatunków rozpoznani i przesortowano prawidłowo,
3. 30 jabłek rozpoznano jako inny gatunek a w rzeczywistości okazało się, że to jest gatunek „X”
4. 20 jabłek innych gatunków rozpoznano nieprawidłowo jako gatunek „X”

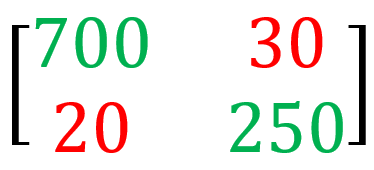
obliczenia

Prec= 700/(700+30)=0,9589

Rec=700/(700+20)=0,9722

F-me= 2*0,9589*0,9722/(0,9589+0,97220= 0,9655 [96,55%]

Klasyfikacja ROC

Istnieje jeszcze inna bardziej precyzyjna metoda klasyfikowania binarnego tzw. krzywa ROC. Powróćmy do rozważań nietypowego przypadku karty kredytowej. Większość algorytmów klasyfikacji zwraca ufność klasyfikacji oznaczoną jako f(X), która z kolei jest wykorzystywana do obliczenia predykcji. Zgodnie z przykładem nadużycia karty kredytowej reguła może wyglądać podobnie do następującej:

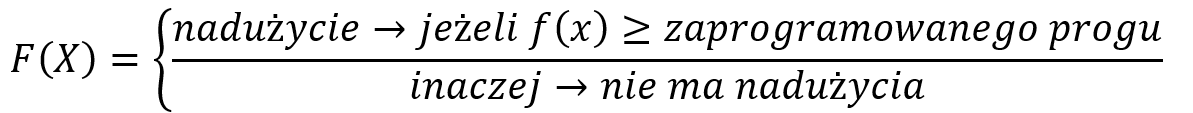
Jeśli tak to próg określa stopę błędu i rzeczywistą stopę dodatnią. Wyniki wszystkich możliwych wartości progowych można wykreślić jako progowe charakterystyki działań Receiver Operating Characteristics (ROC), jak to pokazano na poniższym diagramie:

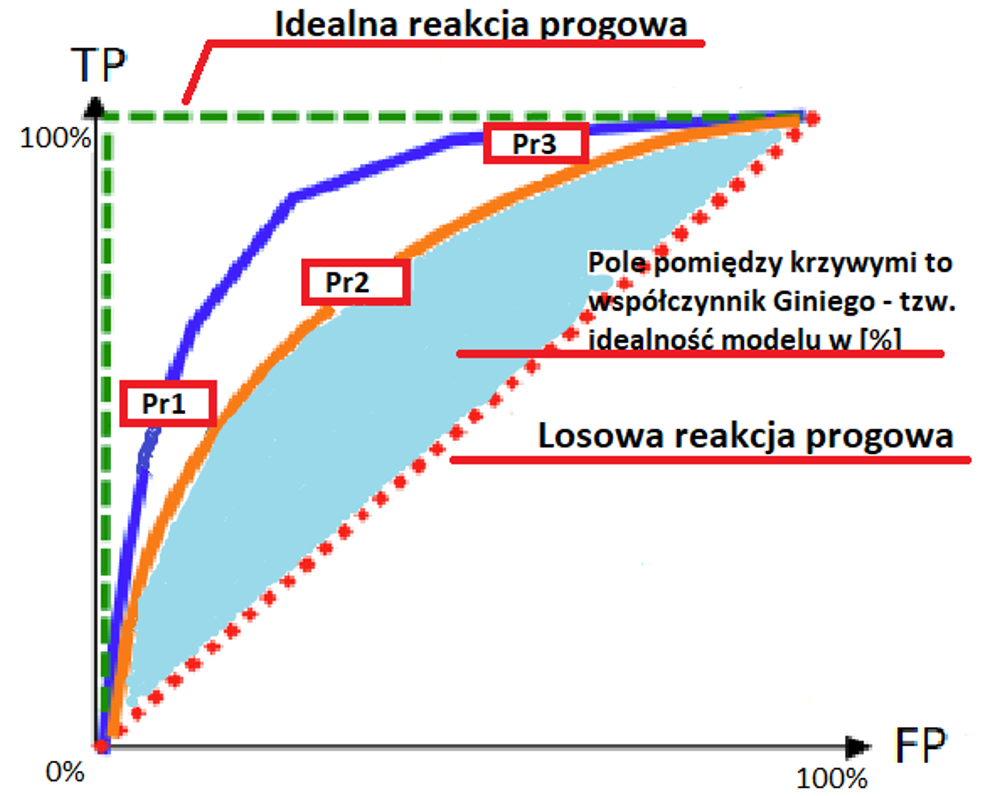
Predykcja losowa jest wykreślona czerwoną linią przerywaną, a predykcja doskonała jest wykreślona zieloną linią przerywaną. Aby np. porównać, czy klasyfikator PR1 jest lepszy niż Pr2, porównujemy obszar pod krzywą, gdzie podstawą jest linia predykcji losowej, im większy obszar pod krzywą tym lepsze jest dopasowania progowe.  Podsumowując krzywa ROC służy do porównania różnych modeli zbudowanych na postawie doboru argumentów czy też na podstawie wyboru różnych metod podejścia do rozwiązania problemu. Zaletą tej metody jest możliwość wizualizacji sytuacji decyzyjnej pod katem wartości progów oraz jakości (zbliżenia przyjętego modelu/algorytmu do ideału).

Przykład:*under construction*

Regresja

Regresja dotyczy ciągłej zmiennej docelowej, w przeciwieństwie do klasyfikacji, która działa z dyskretną zmienną docelową. Na przykład: aby przewidzieć temperaturę zewnętrzną na kilka następnych dni, użyjemy regresji, a klasyfikacja posłuży do przewidzenia, czy będzie padać, czy nie. Ogólnie rzecz biorąc, regresja to proces, który szacuje związek między cechami, czyli jak zróżnicowanie cechy zmienia zmienną docelową. Wynikiem regresji będzie model w postaci funkcji y=f(x).

Regresja liniowa

Najbardziej podstawowy model regresji zakłada liniową zależność między cechami a zmienną docelową. Opisywany jako funkcja y=ax+b. Model jest często dopasowywany przy użyciu metody najmniejszych kwadratów, co oznacza, że najlepszy model minimalizuje kwadraty błędów. W wielu przypadkach regresja liniowa nie jest w stanie modelować złożonych relacji; na przykład poniższy diagram przedstawia cztery różne zestawy punktów o tej samej linii regresji liniowej. Model lewy górny oddaje ogólny trend i można go uznać za właściwy model, natomiast model lewy dolny znacznie lepiej pasuje do punktów (z wyjątkiem jednego odstającego, który należy dokładnie sprawdzić), a górna i dolna prawa strona to liniowe modele, które całkowicie pomijają podstawową strukturę danych i nie mogą być uważane za właściwe modele:

Regresja logistyczna

Regresja liniowa działa, gdy zmienna zależna jest ciągła. Jeśli jednak zmienna zależna ma charakter binarny, czyli 0 lub 1, sukces lub porażka, tak lub nie, prawda lub fałsz, żywy lub zmarły itd. to zamiast regresji liniowej używana jest regresja logistyczna. Jednym z takich przykładów jest próba kliniczna leków, w której badany osobnik albo reaguje na leki, albo nie odpowiada. Jest również używany do wykrywania oszustw, gdzie transakcja jest oszustwem lub nie. Zwykle do pomiaru relacji między zmiennymi zależnymi i niezależnymi używana jest funkcja logistyczna, postrzegana jako rozkład Bernoulliego i po wykreśleniu rzeczywistego przypadku wygląda podobnie do krzywej w kształcie litery „S”. W rzeczywistości stosuje się typowy ogólny zapis matematyczny takiej funkcji który ma postać:

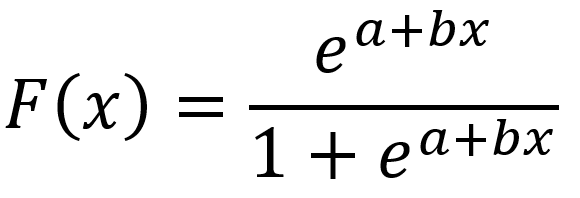
Funkcja F(x) dla przedziału x(-∞, +∞) będzie osiągać wartości F(x) →(0, 1). Możemy zatem powiedzieć, że dla wejściowej zmiennej ciągłej (argumentu) funkcja przyjmuje wartości dyskretne na wyjściu. Przykładowy wykres poniżej:

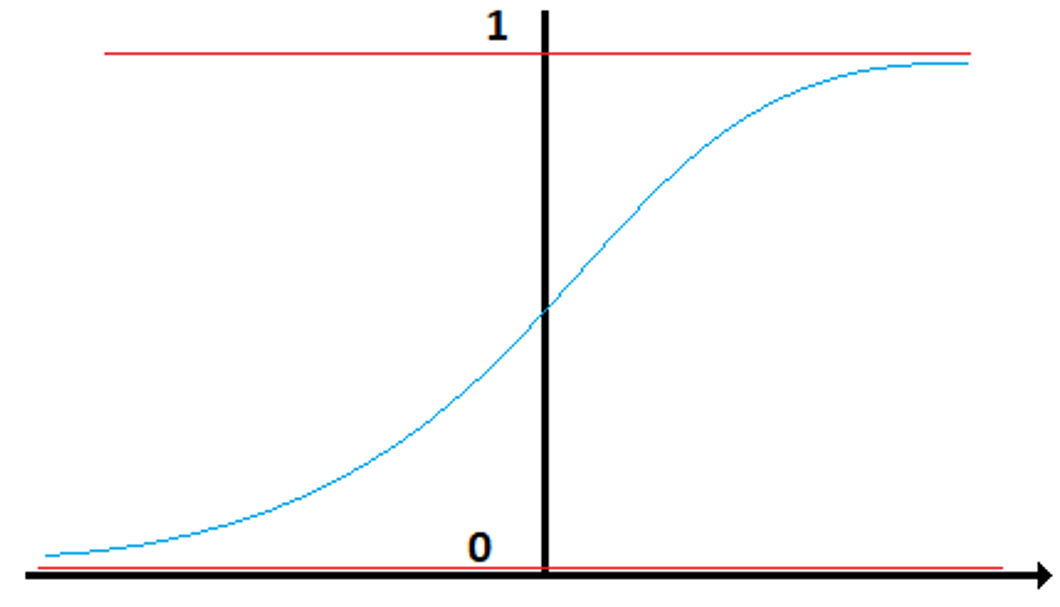
Krzywa „S” będzie posiadała coraz bardziej ostry przebieg na ile w wybranym modelu będzie więcej cech definiujących model lub jednoznaczność decyzyjna będzie po prostu oczywista. Należy o tym pamiętać przy doborze modelu w taki sposób by histereza modelu przebiegała w możliwie najbardziej ostry sposób. Przykładowo o ile w rozpoznawanym obrazie będziemy rozróżniać tylko kolor biały i czarny przy stałym optymalnym oświetleniu np. 1000lx oświetlenie do prac precyzyjnych) to pozyskanie dyskretnego wyniku w odniesieniu do wzorca nie stanowi problemu,  jeśli maszyna uczyła się przy takich warunkach to niekoniecznie zachowa się prawidłowo przy oświetleniu np. 0,2lx czyli przy świetle księżycowym w pełni. Tutaj będzie wymagany inny model i więcej danych pośrednich w uczeniu maszynowym do osiągnięcia poprawnego rezultatu z satysfakcjonującym nas prawdopodobieństwem.

Ocena regresji

W regresji na podstawie otrzymanego z danych pomiarowych modelu przewidujemy wartości zależne Y na podstawie danych wejściowych X. Przewidywania są zwykle obarczone pewnym błędem. Główne pytanie, które musimy sobie zadać, brzmi: o ile? Innymi słowy, chcemy zmierzyć odległość między wartościami przewidywanymi i rzeczywistymi.

• Błąd średnio kwadratowy MSE dla uczenia maszynowego możemy powiedzieć, że błąd średnio kwadratowy to średnia kwadratowa różnicy między wartościami predykcji (prognozy wyliczonej) a rzeczywistej wartości z danych na podstawie których maszyna się uczyła.

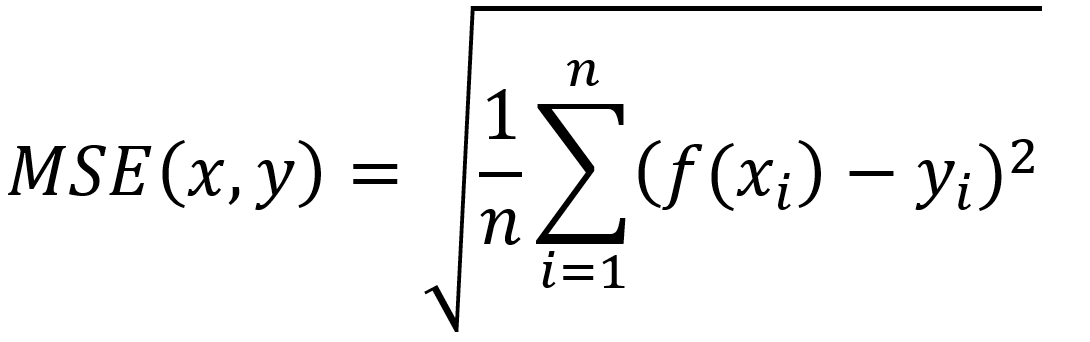
Miara ta jest bardzo wrażliwa na wartości odstające, na przykład 99 dokładnych predykcji i 1 predykcja błędna o 10 jest oceniana tak samo, jak wszystkie predykcje błędne o 1. Co więcej, miara jest wrażliwa na średnią. Dlatego zamiast tego często używany jest błąd względny kwadratowy, który porównuje MSE naszego predyktora z MSE predyktora średniej (który zawsze przewiduje wartość średnią).

• Średni błąd bezwzględny (MAE)to średnia bezwzględnej różnicy między wartościami przewidywanymi i rzeczywistymi. MAE uwzględnia średnią wielkość błędów w zestawie prognoz, bez uwzględniania ich kierunku.

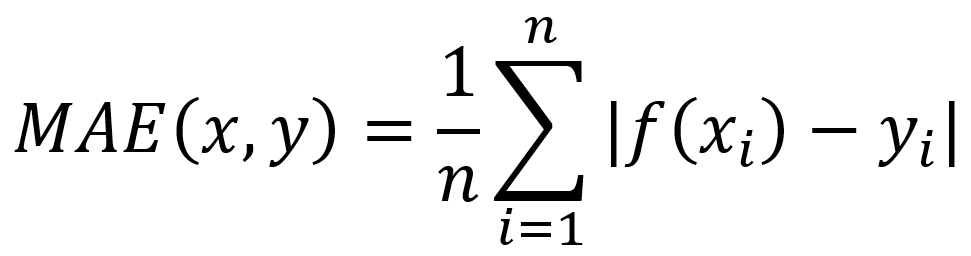
Jest to średnia w postaci bezwzględnych różnic między prognozą a rzeczywistą obserwacją. MAS jest mniej wrażliwy na wartości odstające, ale jest również wrażliwy na średnią i skalę.

• Współczynnik korelacji (CC). Współczynnik korelacji porównuje średnią predykcji względem średniej, pomnożoną przez wartości treningowe względem średniej. Interpretacja: jeśli liczba jest ujemna, oznacza to słabą korelację; liczba dodatnia oznacza silną korelację; a zero oznacza brak korelacji. Korelację między prawdziwymi wartościami x a przewidywaniami y definiuje się następująco:

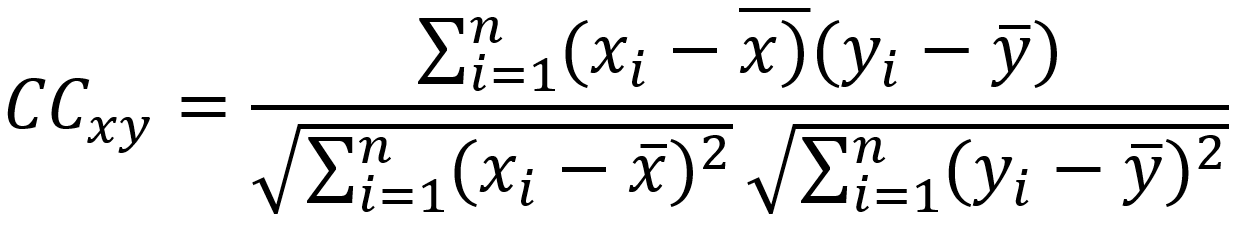
Miara CC jest całkowicie niewrażliwa na średnią i skalę oraz mniej wrażliwa na wartości odstające. Jest w stanie uchwycić względną kolejność, co czyni go przydatnym do rangowania zadań (przydzielanie odpowiedniej rangi poszczególnym obserwacjom w celu ich uszeregowania niezależnie od różnicy wielkości miedzy nimi), takich jak np. trafność dokumentu.

Uogólnienie i ocena

Utworzony model podlega ocenie. Chcemy wiedzieć na ile model jest dokładny oraz jak będzie się zachowywał na nowych danych próby.

Dopasowanie

Trenowanie predyktorów może prowadzić do modeli, które są zbyt złożone lub zbyt proste. Model o niskiej złożoności po lewej (1.) stronie rysunku poniżej może być zbyt prosty by oddać rzeczywiste prognozowane zachowanie, jak i również przewidywanie najczęstszej lub średniej wartości klasy. Również model o dużej złożoności (3.) może reprezentować instancje szkoleniowe ale ze względu na jego zbytnią komplikację raczej słabo nadaje się do wykorzystania praktycznego. Co więcej zbyt skomplikowany model nie odda nam typowej wartości średniej i będzie kompletnie nieprzydatny wydajnościowo do działania w czasie rzeczywistym. Tryby, które są zbyt sztywne, np. pokazany po lewej stronie (1.), nie może uchwycić wzorca, model jest zbyt elastyczny, podczas gdy pokazany po prawej stronie (3.) , gdzie jest już praktycznie jest dopasowany do szumu w danych treningowych będzie zbyt skomplikowany dla rzeczywistego modelu. Głównym wyzwaniem jest dobranie odpowiedniego algorytmu uczenia i jego parametrów, tak aby wyuczony model działał dobrze na nowych danych (środkowa kolumna 2.)

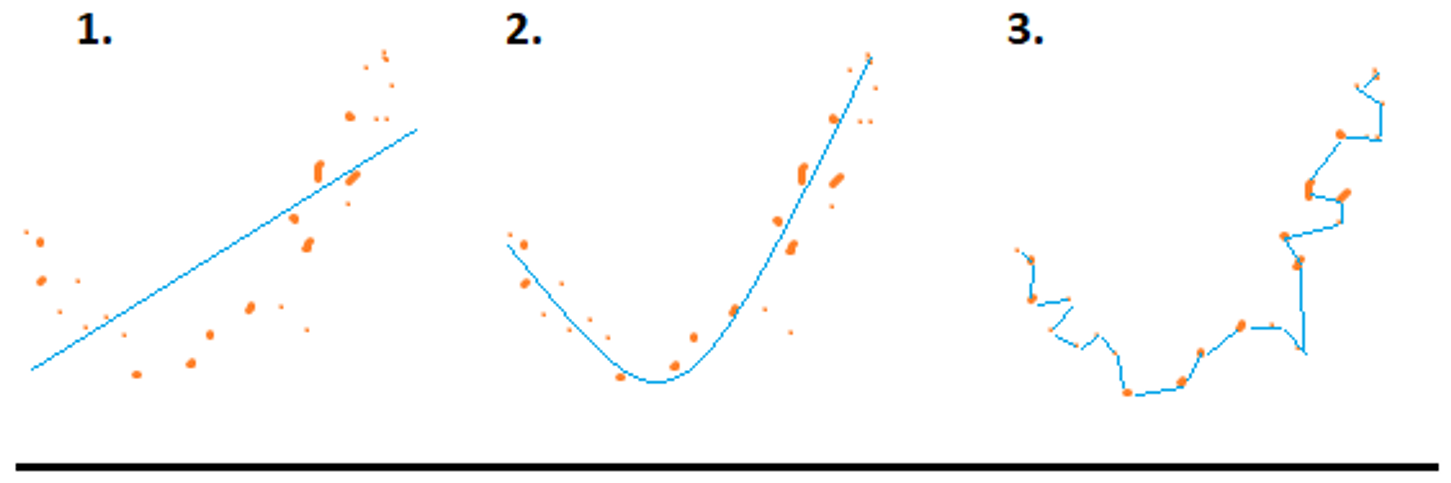
Problem optymalizacji modelu jest ściśle zależny od typu danych i przeznaczenia algorytmu. Uogólniając zagadnienie, pewne wskazówki są na tyle uniwersalne że można je przedstawić w jakimś ogólnym  zestawie wytycznych. Jak wspomniano sztywne modele nie pasują do danych i mają duże błędy. Wraz ze wzrostem złożoności modelu model lepiej opisuje podstawową strukturę danych uczących, a w konsekwencji zmniejsza się błąd. Jeśli model jest zbyt złożony, przepełnia dane treningowe, a jego błąd przewidywania ponownie wzrasta:

Ocena i optymalizacja

W zależności od złożoności zadania i dostępności danych chcemy dostroić nasze klasyfikatory do mniej lub bardziej złożonych struktur. Większość algorytmów uczących umożliwia takie dostrajanie w taki sposób by uzyskać optimum. Ogólne zależności przedstawiono poniżej.

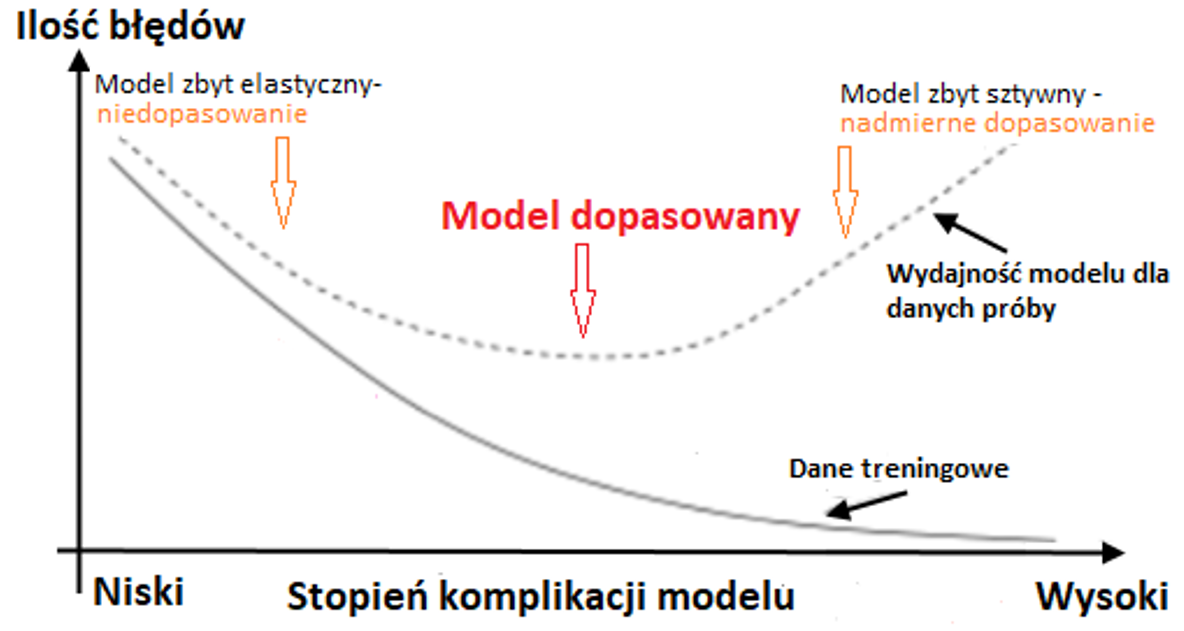
Wskazówką stopnia komplikacji mogą być omawiane wcześniej struktury algorytmów w uproszczonym zestawieniu

Dane treningowe i testowe.

Dobór danych treningowych i testowych

Aby oszacować błąd uogólnienia, dzielimy nasze dane na dwie części: dane treningowe i dane testowe. Ogólną zasadą jest dzielenie ich według proporcji trening vs test, typowo 70:30. Najpierw trenujemy predyktor (generujemy model) na danych uczących (treningowych) a następnie przewidujemy wartości dla danych testowych, a na końcu obliczamy błąd, czyli różnicę między wartościami przewidywanymi i rzeczywistymi.

Takie podejście daje nam możliwość oszacowania prawdziwego błędu uogólnienia. Szacowanie opiera się na dwóch następujących założeniach: po pierwsze, zakładamy, że zestaw testowy jest bezstronną próbką z naszego zbioru danych, a po drugie, zakładamy, że rzeczywiste nowe dane ponownie złożą dystrybucję jako nasze przykłady szkoleniowe i testowe. Pierwsze założenie można złagodzić poprzez walidację krzyżową i stratyfikację. Ponadto, jeśli jest ich mało, nie można pozwolić sobie na pominięcie znacznej ilości danych dla oddzielnego zestawu testowego, ponieważ algorytmy uczące nie działają dobrze, jeśli nie otrzymują wystarczającej ilości danych. W takich przypadkach zamiast tego używana jest walidacja krzyżowa.

Walidacja krzyżowa

Weryfikacja krzyżowa dzieli zbiór danych na k-zestawów o mniej więcej tej samej wielkości. Najpierw używamy zestawów od 2 do 5 do nauki i zestawu 1 do treningu. Następnie powtarzamy procedurę pięć razy, pomijając jeden zestaw na raz do testowania i uśredniamy błąd w pięciu powtórzeniach:

Elementy zbiorów danych, wyszukiwanie zależności w odniesieniu do typu zbioru – „odległości” między danymi

Wiele problemów można sformułować jako znalezienie podobnych zestawów elementów.  Na przykład klienci, którzy kupili podobne produkty, strony internetowe o podobnej treści, obrazy z podobnymi obiektami, użytkownicy, którzy odwiedzili podobne witryny itd. Jeśli tak, dwa elementy są uważane za podobne, jeżeli są w niewielkiej odległości od siebie. Główne pytania dotyczą tego, jak każdy element jest reprezentowany i jak definiowana jest odległość między elementami. Istnieją dwie główne klasy miar odległości:

• Odległości euklidesowe
• Odległości nieeuklidesowe

Odległości euklidesowe

Odległość euklidesowa, jest najczęściej stosowaną miarą odległości, która mierzy odległość od siebie dwóch przedmiotów np. w dwuwymiarowej przestrzeni (płaszczyzn może być więcej natomiast tutaj rozważymy przestrzeń dwuwymiarową). Oblicza się go w następujący sposób:

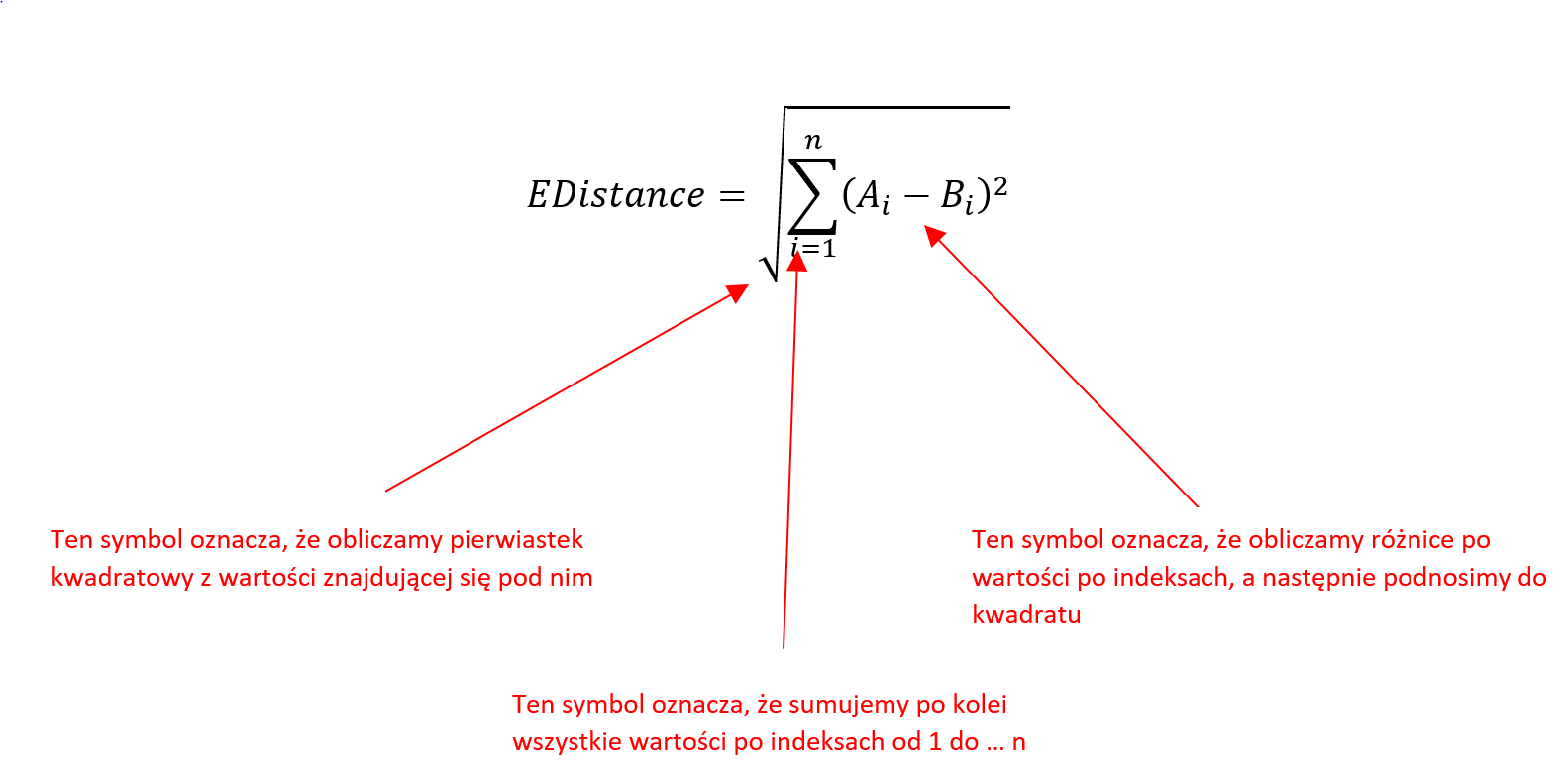
Przykładowe obliczenie w excel dla wektorów A(3,8,19) oraz B(7,12,22)  daje wynik EDistance=6,40

Sprawdź w excel

Odległości nieeuklidesowe

Odległość nieeuklidesowa opiera się nie na ich lokalizacji w przestrzeni, a na właściwościach poszczególnych elementów zbioru danych. Najbardziej znane odległości to odległość Jaccarda, odległość cosinusowa, odległość Levenshteina (edycyjna) i odległość Hamminga.

Odległość Jaccarda

Odległość Jaccarda służy do obliczania odległości między dwoma zestawami danych. Obliczamy podobieństwo Jaccarda dwóch zbiorów jako rozmiar ich przecięcia podzielony przez rozmiar ich sumy,

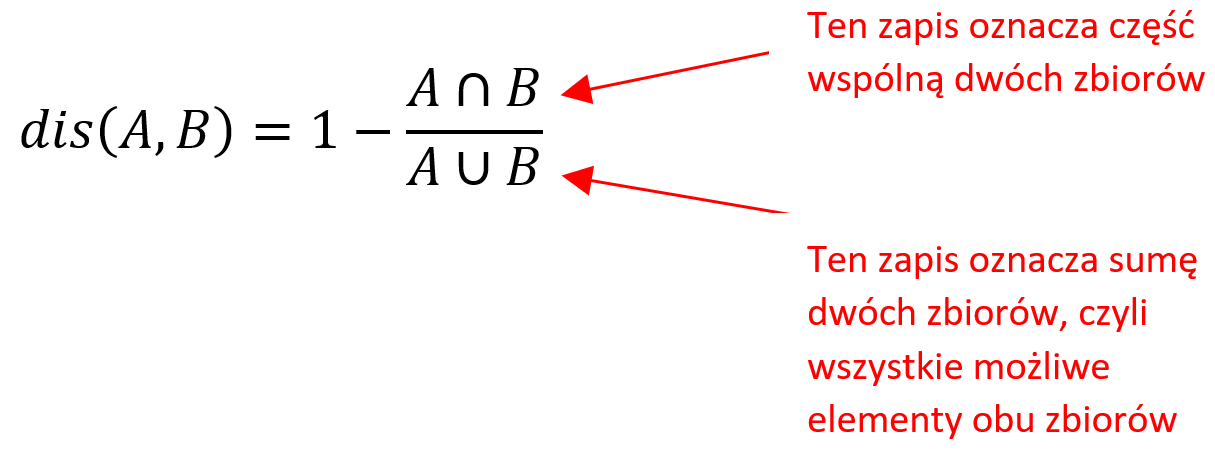
Łatwo zauważyć że odległość Jaccarta używamy do określenia zgodności dwóch zbiorów danych (niekoniecznie liczb) Jeżeli zbiory są zgodne to Jdistance=0, jeżeli zbiory nie mają elementów wspólnych Jdistance=1.

Przykładowe obliczenie w excel dla wektorów A(3,8,12,19) oraz B(7,12,19,22, 29, 34, 42) daje wynik JDis=0,77

Sprawdź w excel

Odległość cosinusowa

Odległość kosinusowa między dwoma wektorami skupia się na orientacji, a nie na wielkości, dlatego dwa wektory o tej samej orientacji mają podobieństwo cosinusowe 1 a odległość równą 0, podczas gdy dwa wektory prostopadłe mają podobieństwo cosinusowe równe 0, a odległość równą 1. Matematycznie obliczamy cosinus kąta między dwoma wektorami rzutowanymi w wielowymiarowej przestrzeni. Odległość cosinusowa jest powszechnie stosowana w wielowymiarowej przestrzeni cech; na przykład w eksploracji tekstu, gdzie dokument tekstowy reprezentuje instancję, cechy, które odpowiadają różnym słowom, a ich wartości odpowiadają liczbie przypadków, w których słowo pojawia się w dokumencie. Obliczając podobieństwo cosinusowe, możemy zmierzyć prawdopodobieństwo dopasowania dwóch dokumentów w opisie podobnej treści.

Wzór ogólny ma postać:

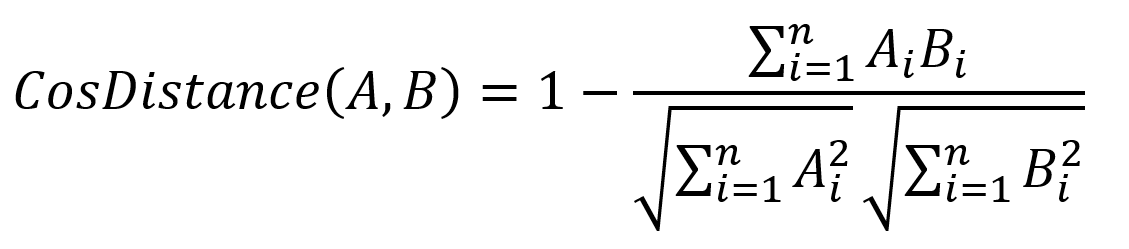
Przykładowe obliczenie w exel dla dwóch wektorów A(3, 8, 19) oraz B(9, 24, 57) daje wynik CosDistance=0 co oznacza ze wektory maja te samą orientację.

Sprawdź w excel

Odległość Levenshteina (edycyjna)

Edycyjna odległość ma sens, gdy porównujemy dwa ciągi. Odległość między łańcuchami a = a1, a2, a3, … an i b = b1, b2, b3, … bn to najmniejsza liczba operacji wstawiania / usuwania pojedynczych znaków wymaganych do konwersji ciągu z b do a, na przykład a = abcd i b = abbd. Aby zamienić b na a, musimy usunąć drugie b i wstawić c w jego miejsce. Taka zamiana wymaga co najmniej 2 operacji stąd odległość Levdistance=2. Najbardziej istotnym wnioskiem jest fakt, iż w przypadku takich samych ciągów (takich samych wyrazów) odległość wynosi Levdistance=0.

Odległość Hamminga

Odległość Hamminga porównuje dwa wektory o tej samej wielkości i oblicza liczbę wymiarów, w których się różnią. Innymi słowy, mierzy liczbę podstawień wymaganych do konwersji jednego wektora na inny.

Przykładowe obliczenie w exel dla wektora A [3, 8, 19, 31] oraz wektora B [7, 8, 22, 31] odległość Hamminga wynosi Hamdistance=2

Sprawdź w excel

Istnieje wiele miar odległości skupiających się na różnych właściwościach, na przykład

• jak korelacja, która mierzy liniową zależność między dwoma elementami,
• jak odległość Mahalanobisa która mierzy odległość między punktem i rozkładu innych punktów,
• jak SimRank, który jest oparty na teorii grafów i mierzy podobieństwo struktury, w której występują badane elementy i tak dalej….

Omówiono najczęściej stosowane miary odległości/podobieństwa pomiędzy zbiorami.


Wybór i zaprojektowanie odpowiedniej miary podobieństwa dla rozwiązywanego problemu to więcej niż połowa sukcesu.

Architektura aplikacji uczenia maszynowego

Struktura aplikacji ML(machine learning)

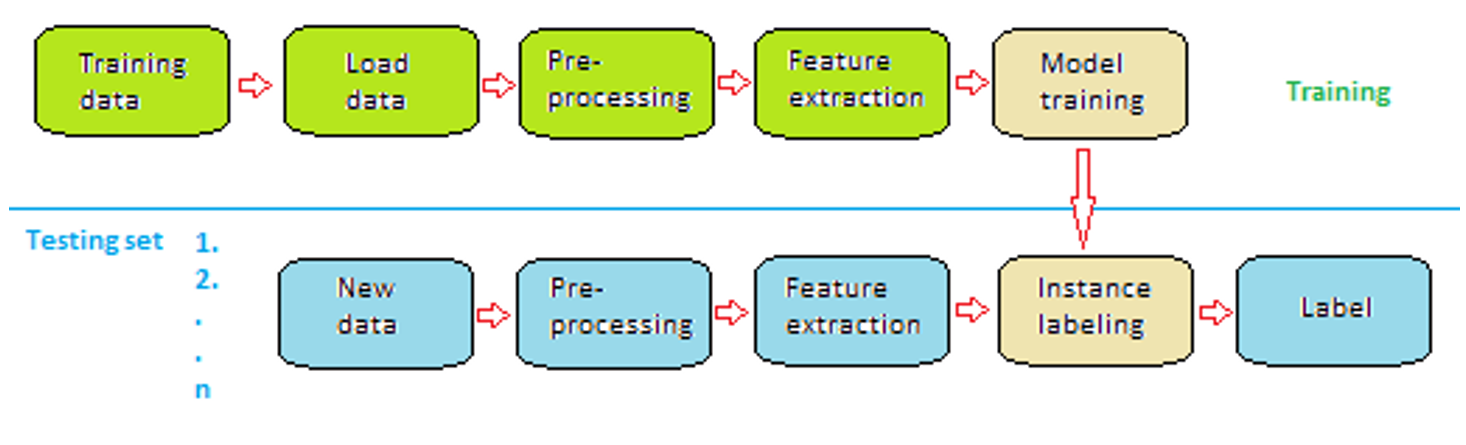
Aplikacje uczenia maszynowego, zwłaszcza te, które koncentrują się na klasyfikacji, zwykle korzystają z tego samego przepływu pracy wysokiego poziomu, który pokazano na poniższym diagramie. Przepływ pracy składa się z dwóch faz — szkolenia klasyfikatora i klasyfikacji nowych instancji. Obie fazy mają wspólne kroki.

Opis struktury trenowania

• Training Data wyodrębniamy zestaw danych do trenowania z bazy danych lub innych zasobów
• Load Data uruchamiamy proces pobrania danych przez aplikacje API
• Pre-procesing wstępnie dostosowujemy dane do przetwarzania w tym przetwarzamy brakujące dane do zastosowanych algorytmów
• Feature extraction wyodrębniamy (uwypuklamy) niektóre cechy danych/wektorów dla zastosowanych algorytmów
• Model training trenujemy (tworzymy) model docelowy

Opis struktury fazy drugiej tj testowania/zachowania modelu

• New Data przygotowanie zestawu danych testowania
• Pre-procesing wstępnie dostosowujemy do przetwarzania w tym przetwarzamy brakujące dane
• Feature extraction wyodrębniamy (uwypuklamy) niektóre cechy danych/wektorów dla zastosowanych algorytmów
• Instance labeling utworzenie nowej instancji testowej i opisanie. Dane opisane etykietą, okresowo ponownie służą dla fazy uczenia, tak by w uzasadnionych przypadkach ponownie nauczyć model i zastąpić stary model ponownie nauczonym w fazie klasyfikacji. Istotne jest by w tym zakresie stworzyć kompleksowe zestawy danych testujących i tworzyć nowe zestawy Testing set 1., Testing set 2. …itd. Jest to swoista biblioteka opisanych danych testowych dla rozpatrywanego zagadnienia.
• Labeling opisy instancji testowych

Tradycyjna architektura uczenia maszynowego

Dane strukturalne, takie jak dane transakcyjne, klientów, analityczne i rynkowe, zwykle znajdują się w lokalnej relacyjnej bazie danych. Biorąc pod uwagę język zapytań, taki jak SQL, możemy wykonać zapytanie dotyczące danych używanych do przetwarzania, jak pokazano w przepływie pracy na poprzednim diagramie.

Zazwyczaj wszystkie dane mogą być przechowywane w pamięci i dalej przetwarzane za pomocą biblioteki uczenia maszynowego, takiej jak Weka, Java-ML lub MALLET. Powszechną praktyką w projektowaniu architektury jest tworzenie potoków danych, w których różne etapy przepływu pracy są dzielone. Na przykład, aby utworzyć rekord danych klienta, być może będziemy musieli zebrać dane z różnych źródeł danych. Rekord może być następnie zapisany w pośredniej bazie danych do dalszego przetwarzania. W takim przypadku należy zaplanować odpowiednia przestrzeń cyfrową dla przechowywania planowanej ilości danych.

Typowe problemy z dużymi danymi i sposoby realizacji projektów

Wielkie zbiory danych istniały na długo przed wynalezieniem frazy Big Data. Na przykład banki i giełdy od lat przetwarzają miliardy transakcji dziennie, a linie lotnicze dysponują infrastrukturą czasu rzeczywistego na całym świecie do operacyjnego zarządzania rezerwacjami pasażerów. Czym więc tak naprawdę są duże zbiory danych? Doug Laney (2001) zasugerował, że duże zbiory danych są definiowane przez trzy V: objętość, prędkość i różnorodność (ang. Volume, Velocity, Variety). Dlatego, aby odpowiedzieć na pytanie, czy nasze dane są duże, możemy to przełożyć na następujące trzy pytania podrzędne:

• Czy możesz przechowywać swoje dane w pamięci, do której masz bezpośredni dostęp?
• Czy możesz przetwarzać nowe przychodzące dane za pomocą jednej maszyny?
• Czy Twoje dane pochodzą z jednego źródła?

Jeśli na wszystkie te pytania odpowiedziałeś twierdząco, to prawdopodobnie nasze dane nie są duże i właśnie uprościłeś architekturę aplikacji.

Jeśli Twoja odpowiedź na wszystkie te pytania brzmiała „nie”, to Twoje dane są duże! Jeśli jednak masz mieszane odpowiedzi, to jest to skomplikowane.

Z punktu widzenia uczenia maszynowego istnieje zasadnicza różnica w implementacji algorytmu w celu przetwarzania danych w pamięci lub z pamięci rozproszonej. Dlatego praktyczna zasada brzmi: jeśli nie możesz przechowywać danych w pamięci, do której masz bezpośredni dostęp, powinieneś zajrzeć do biblioteki uczenia maszynowego Big Data. Dokładna odpowiedź zależy od problemu, który próbujesz rozwiązać. Co do zasady wytwórczej, nowy projekt, powinniśmy zacząć od biblioteki dla jednej maszyny i prototypu planowanego algorytmu, być może z podzbiorem danych, jeśli całe dane nie mieszczą się w dostępnej pamięci. Po potwierdzeniu dobrych założeń początkowych do dalszej rozwagi można przeanalizować przejście na coś więcej jak np. Mahout lub Spark

Architektura aplikacji Big Data

Duże zbiory danych, takie jak dokumenty, blogi internetowe, sieci społecznościowe, dane z czujników i inne, są przechowywane w bazie danych NoSQL (Not only SQL), takiej jak MongoDB, lub w rozproszonym systemie plików, takim jak HDFS. W przypadku, gdy mamy do czynienia z danymi strukturalnymi, możemy wdrożyć możliwości baz danych za pomocą systemów takich jak Cassandra lub HBase, które są zbudowane na Hadoop. Przetwarzanie danych odbywa się zgodnie z paradygmatem MapReduce, który dzieli problemy z przetwarzaniem danych na mniejsze pod problemy i rozdziela zadania między węzły przetwarzania. Modele uczenia maszynowego są ostatecznie trenowane za pomocą bibliotek uczenia maszynowego, takich jak Mahout i Spark .
MongoDB to baza danych NoSQL, która przechowuje dokumenty w formacie podobnym do JSON. Więcej na ten temat można przeczytać na https://www.mongodb.com/.
Hadoop to platforma do rozproszonego przetwarzania dużych zbiorów danych w klastrze komputerów. Zawiera własny format systemu plików, HDFS, strukturę planowania zadań, YARD i implementuje podejście MapReduce do równoległego przetwarzania danych. Więcej informacji o Hadoop można znaleźć pod adresem https://hadoop.apache.org/.  
Cassandra to system zarządzania rozproszoną bazą danych, który został stworzony, aby zapewnić odporną na awarie, skalowalną i zdecentralizowaną pamięć masową. Więcej informacji można znaleźć na https://cassandra.apache.org/.  
HBase to kolejna baza danych, która koncentruje się na losowym dostępie do odczytu/zapisu dla rozproszonej pamięci masowej. Więcej informacji można znaleźć na stronie https://hbase.apache.org/.

Klasyfikacja

Klasyfikacja podstawowe informacje

Klasyfikacja jest stosowana w uczeniu nadzorowanym w którym maszyna ucząc się na podstawie danych wejściowych tworzy nową obserwację lub klasyfikuje dane do jakiejś klasy (grupy).

Najczęściej jednak klasyfikacja to proces kategoryzacji danego zbioru danych na klasy. Może być przeprowadzana zarówno na danych ustrukturyzowanych, jak i nieustrukturyzowanych. Proces rozpoczyna się od przewidzenia klasy danych punktów. Klasy są często określane jako cel, etykieta lub kategoria.

Przy takim podejściu w efekcie końcowym otrzymujemy model prognozy klasyfikacji (tj przydzielania nowych danych do różnych klas) opierający się na aproksymacji funkcji odwzorowania ze zmiennych wejściowych ciągłych i/lub dyskretnych na dyskretne zmienne wyjściowe. Głównym celem jest określenie, do której klasy/kategorii będą należały nowe dane. Klasyfikacja jest znacznym uproszczeniem i przyspieszeniem procesów decyzyjnych opracowywanych algorytmów.

Przykład:             dane ciągłe na dyskretne – (ciągła) temperatura poniżej 20^oC – (dyskretna) za zimno, temperatura powyżej 30^oC – za ciepło

                               dane dyskretne na dyskretne – (dyskretna) litera „a” – (dyskretna) samogłoska

W pierwszym przypadku otrzymujemy sklasyfikowanie skali temperatury na trzy klasy [za zimno], [OK], [za ciepło], w drugim przypadku otrzymujemy sklasyfikowanie alfabetu na dwie klasy [samogłoska], [spółgłoska].

Terminologia i definicje stosowane w klasyfikacji

• Klasyfikator – algorytm/metoda/technika użyta do zmapowania danych wejściowych na określone klasy/grupy/kategorie wyjściowe.
• Model klasyfikatora – model prognozowania lub wnioskowania danych treningowych do przydzielania w zakresie generowanych klas lub zdyskretyzowanych wartości wniosków wyjściowych.
• Cecha – mierzalna właściwość obserwacji
• Klasyfikacja binarna – klasyfikacja która na wyjściu może posiadać stany logiczne np. [ma]-[nie ma], [0]-[1], [prawda-fałsz].
• Klasyfikacja wieloklasowa – klasyfikacja, która ma więcej niż dwie klasy na wyjściu jest klasyfikacja wieloklasową. Klasyfikacja wieloklasowa musi spełniać warunek, iż każda dana wejściowa na wyjściu może być przypisana tylko do jednej z klas wyjściowych lub wniosku
• Klasyfikacja etykietowana – w tym przypadku każda z danych może być przypisana do więcej niż jednej klasy lub wniosku decyzyjnego w zależności od przypisanej etykiety(opisu).

Rodzaje metod uczenia stosowane w klasyfikatorach

• Uczenie leniwe (lazy learn) – klasyfikacja odbywa się przy użyciu najbardziej powiązanych danych w przechowywanych danych treningowych. To oznacza, że w pierwszym kroku uruchamiamy kwerendę w obsługiwanej bazie danych SQL i po jej zwrocie otrzymane wstępnie przygotowane dane służą do klasyfikacji. Typowy przykład algorytmu k-nearest neighbor.
• Uczenie chętne (eager learn) – klasyfikacja odbywa się na zasadzie przetwarzania wszystkich danych wejściowych wg wstępnie przyjętej hipotezy. Typowy przykład sztuczne sieci neuronowe, drzewa decyzyjne.

Drzewo decyzyjne

Informacje ogólne

Jedną z najbardziej intuicyjnych metod klasyfikacji i predykcji jest drzewo decyzyjne. Główną cechą tej metody jest fakt, iż najczęściej jest ona oparta o hipotetyczne reguły, a nie o parametry. Uszczegóławiając wcześniej omawianą strukturę drzewa należy zauważyć, że istotnym elementem budowania zależności jest sposób trenowania (obliczania decyzji) na podstawie danych węzła.

Dodatkowe pojęcia związane z drzewem decyzyjnym – ENTROPIA. Entropia to upraszczając swoista czystość danych w danym węźle. Zasada jest następująca – im dane są bardziej „czyste” (bardziej jednoznaczne) tym niższa jest wartość entropii.

Przykład obliczenia entropii. Mamy ankietę wypełnioną przez 100 kierowców pewnego miasta K z 1 pytaniem, którą trasą „A” czy „B” pojedziesz do miasta W z miasta K”. 70 kierowców odpowiedziało „A” pozostali zaprzeczyli. Czyli mamy następujące dane jako zbiór próby X, która składa się ze 100 danych w tym 70 danych z poziomem true, oraz 30 danych z poziomem false. Dodatkowo jest jedna dana ukryta (czy może raczej domyślna), ilość klas m=2, czyli klasyfikacja binarna. Entropia jest opisana wzorem:

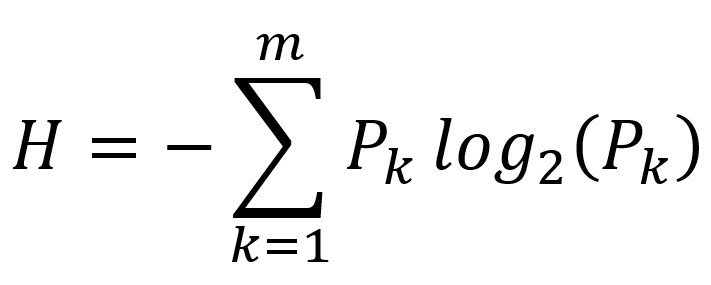
Gdzie P_k jest prawdopodobieństwem wystąpienia określonej klasy. Przykładowe obliczenie entropii w excel.

Uwaga – w naszym przypadku log_2, ponieważ mamy m=2 klasy. Wartość podstawy logarytmu powinna odpowiadać ilości klas jeżeli chcemy normalizacji, by nasze wyniki obliczeń należały do zbioru liczb R₊(0,1>.

Dla omawianego przykładu H=0,881. Co to właściwie oznacza? Dla porównania policzmy jeszcze entropię dla podziału w ankiecie 50/50 oraz 99/1. Obliczone odpowiednio H=1 oraz H=0,08~0. Zatem mamy trzy entropie węzłowe 1; 0,88; 0,08. To jaką trasą pojedziemy (lub jaką trasą poprowadzi nas sztuczna inteligencja w oparciu o dane) zależeć będzie od decyzji, którą podejmiemy na podstawie obliczeń. Przykładowo dla H=1 będziemy się wahać a nawigacja wskaże nam dwie możliwe trasy do wyboru lub wybierze losowo. Dla H=0,88 będzie to wskazanie na trasę „A” aczkolwiek sami widzimy, że to jest jednak bardziej wskazanie a nie jednoznaczna decyzja. Nie ma jednak żadnych wątpliwości dla H→0, tylko trasa „A”.

Wracając do interpretacji „czystości” danych. Najmniej korzystna sytuacja to taka, gdzie entropia wynosi „1”. Oznacza to, że wartość decyzyjna węzła w drzewie jest praktycznie żadna. Należy zatem podczas tworzenia drzewa decyzyjnego unikać takich węzłów, gdzie zawarte są węzły o wartości entropii = 1. Czasami wskazana jest analiza danych i taka ich modyfikacja, która pozwoli na optymalizację.

Dodatkowe pojęcia związane z drzewem decyzyjnym – Zysk informacji

Zysk informacji to koncepcja, której głównym celem jest oszacowanie informacji i można uzyskać poprzez rozdzielenie bieżącego badanego zbioru danych w odniesieniu na atrybuty. Zysk informacji jest zdefiniowany jako różnica pomiędzy entropią zmiennej (węzła), a entropia atrybutu pochodzącego od tego węzła (rozgałęzienia). Powyższe można opisać wzorem jak poniżej:

Dodatkowe pojęcie związane z drzewem decyzyjnym – Współczynnik zysku informacji

Ponieważ może się zdarzyć, że wzajemne różnice dla obliczeń zysku informacji mogą być nieznaczne, a co za tym idzie niezauważalne można zastosować zabieg uwypuklający nieznaczne różnice. Aby zredukować takie nastawienie, można zastosować „współczynnik wzmocnienia”. Współczynnik wzmocnienia dla atrybutu jest zdefiniowany jako:

współczynnik wzmocnienia atrybutu = zysk-informacja-atrybut / informacja-wewnętrzna-atrybut

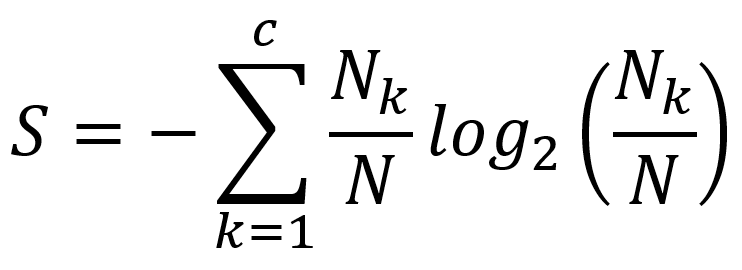
Algorytm

• Dane wejściowe. Zbiór danych wejściowych należy przygotować w tabeli dwuwymiarowej. Wszystkie atrybuty należy umieścić w kolumnach, z opcja sortowania po kolumnach (atrybutach). Dla ułatwienia najlepiej kolumnę wyników umieścić jako końcowa po prawej stronie
• Dane wyjściowe struktura drzewa zakończona liśćmi.
• Wykonaj w pętli kolejne kroki:
  • Oblicz entropię dla całości danych
  • Posortuj dane wyjściowe dla każdego argumentu wg danych kolumny wyjściowej
  • Dla każdego rozgałęzienia (związanego z węzłem-atrybutem) oblicz zysk informacji
    • W przypadku koniecznym oblicz dodatkowo współczynnik zysku informacji
  • Wyznacz węzeł (węzły) i powróć do pkt 1
• Powtarzaj czynność dla każdego nowego węzła aż do osiągnięcia poziomu liści tj. kiedy węzeł zakończy się liśćmi jako elementami z kolumny wyników.
• Jeśli wynik jest niesatysfakcjonujący przeanalizuj inną konfigurację argumentów lub zmodyfikuj dane.

Kompletny przykład obliczeń w Excel całego drzewa oraz obliczeń cząstkowych „H”, „G”, „S” w pliku.
Sprawdź w excel.

Predykcja liniowa

Informacje ogólne

Regresja liniowa to model predykcyjny (prognostyczny) , w którym dane uczące są wykorzystywane do konstruowania modelu liniowego w celu przewidywania wartości wynikowej dla określonych atrybutów. Kiedy mówimy o modelu liniowym, mamy na myśli to, że związek między wartością docelową (zmienną zależną) a atrybutem (zmiennymi niezależnymi) jest liniowy. W analizie regresji liniowej może występować jedna lub więcej zmiennych niezależnych. Gdy istnieje tylko jedna zmienna niezależna, model liniowy wyraża się powszechnie obserwowaną funkcją liniową y = mx + b, gdzie y jest zmienną zależną, m jest nachyleniem prostej, a b jest punktem przecięcia osi 0Y dla atrybutu x=0. W większości przypadków istnieje więcej niż jedna zmienna niezależna; dlatego model liniowy jest reprezentowany jako y = m₁x₁ + m₂x₂ + … + m_nx_n + b, gdzie jest n zmiennych niezależnych, a m_i jest współczynnikiem związanym z określoną zmienną niezależną x_i, dla i = 1 … n. Aby skonstruować taki model liniowy, musimy znaleźć wartości m_i i b na podstawie znanych wartości y(x_i) w uczącym zbiorze danych. W naszym przypadku obliczymy ręcznie zależność funkcji od jednej zmiennej.

Przykład Sprzedajesz lody na plaży w Sopocie i chciałbyś wiedzieć ile zamówić, żeby sprzedać maksymalna ilość towaru tak by nie zostać z niesprzedanym towarem w pojemniku który jak wiadomo stopnieje i będzie stratą. Chciałbyś w pierwszym kroku zastanowić się nad prognozowaniem sprzedaży lodów na podstawie prognozy pogody. Zebrałeś pewne dane, które wiążą uśrednione tygodniowo wysokie temperatury w ciągu dnia ze sprzedażą lodów w sezonie letnim. Zebrane dane uczące uporządkowane w tabeli są następujące.

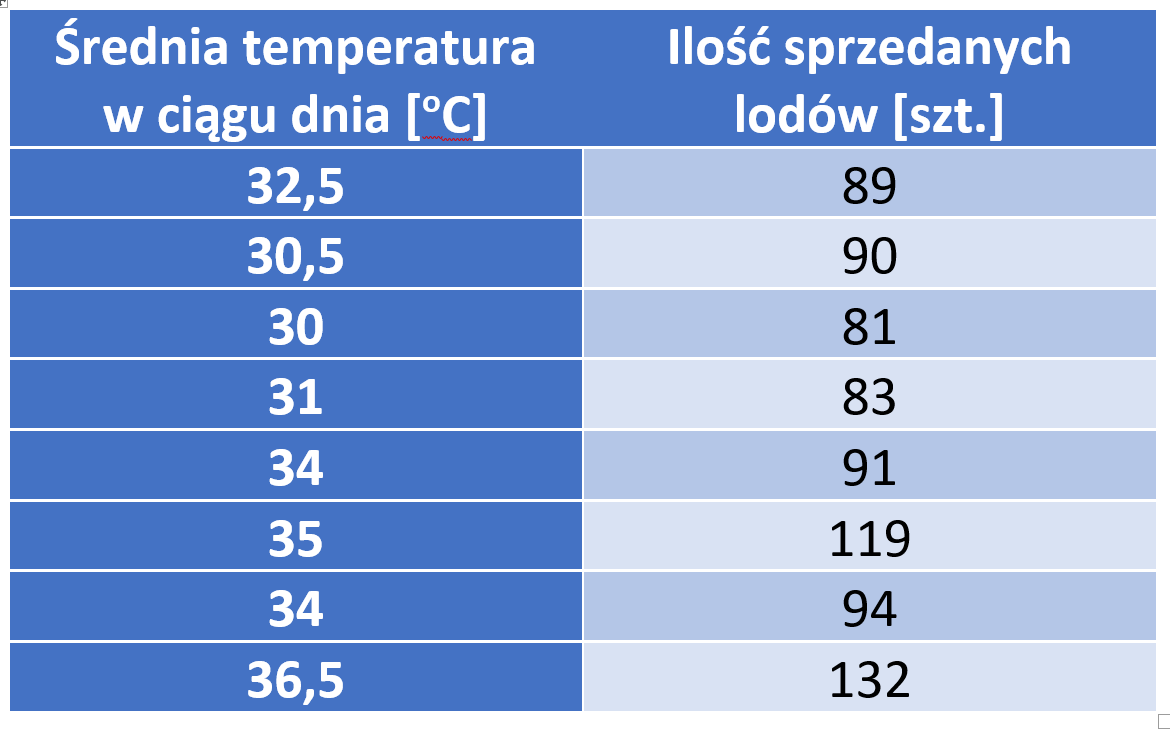
Jak wspomniano naszym celem jest wyznaczenie modelu jako ogólnego równania o uśrednionej postaci

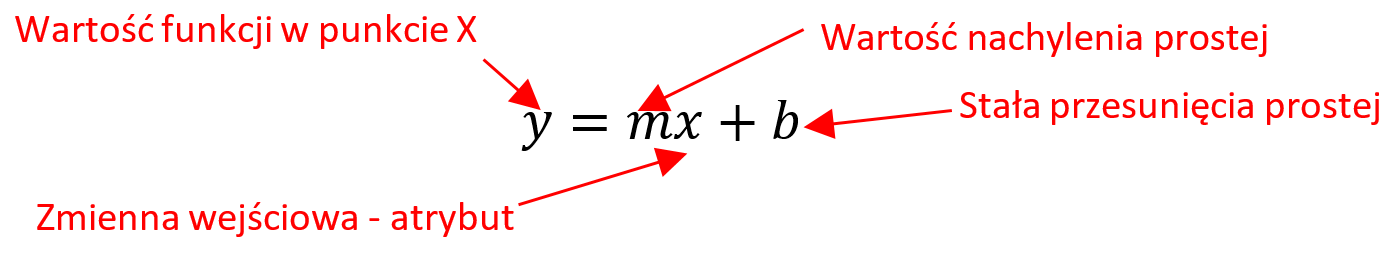
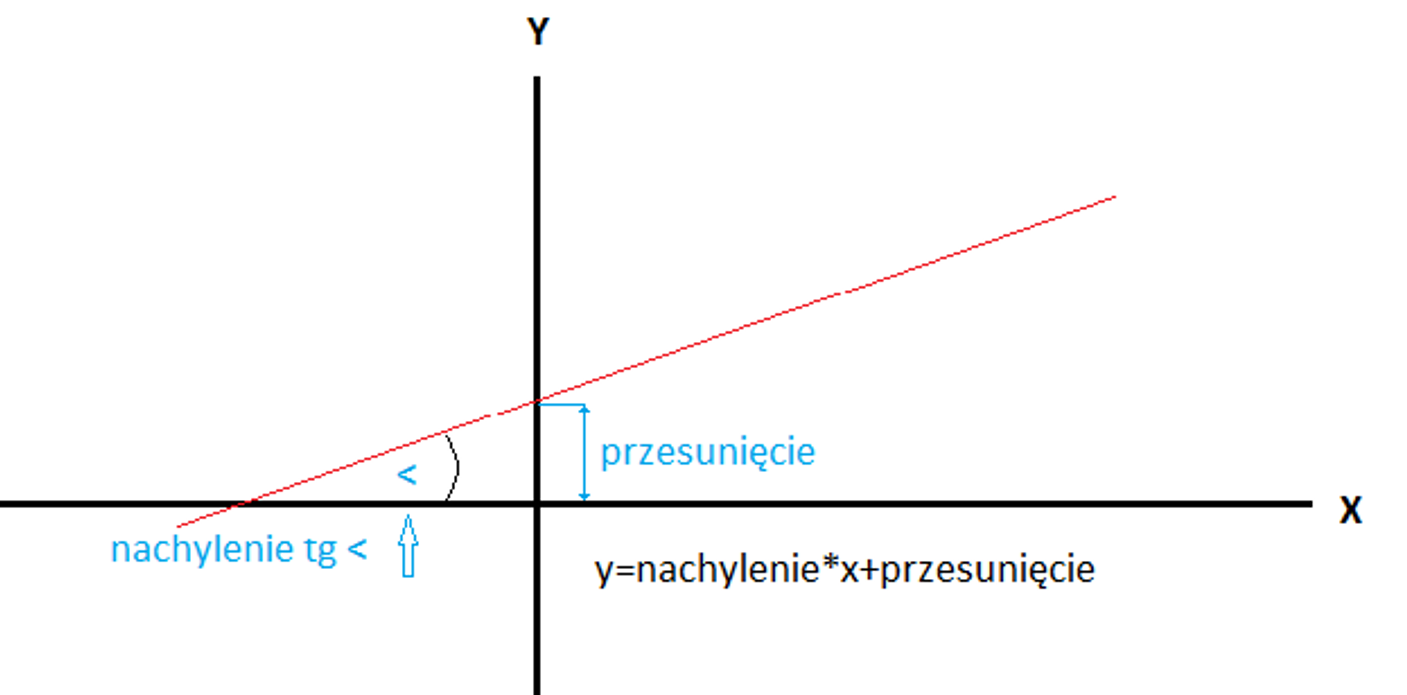
Można skorzystać z gotowej funkcji w Excel „obliczenie linii trendu”, ale w naszych rozważaniach ważny jest element poznawczy zagadnienia i w tym przypadku skorzystamy z obliczeń wykonanych ręcznie. Ponieważ do obliczeń stosujemy metody uśredniające, jako fakt możemy przyjąć, że wartość uśredniona nie koniecznie będzie w 100% zbieżna w każdym punkcie atrybut – wynik, ale może również leżeć w jego otoczeniu co oznacza, że nasza predykcja będzie obarczona pewnym błędem. By oszacować dokładność naszego modelu musimy obliczyć współczynnik determinacji R². Zrozumienie istoty tego współczynnika jest proste o ile spojrzymy na wzór od strony graficznej. Ogólna postać współczynnika determinacji ma postać

gdzie regresyjna suma kwadratów jest opisana wzorem:

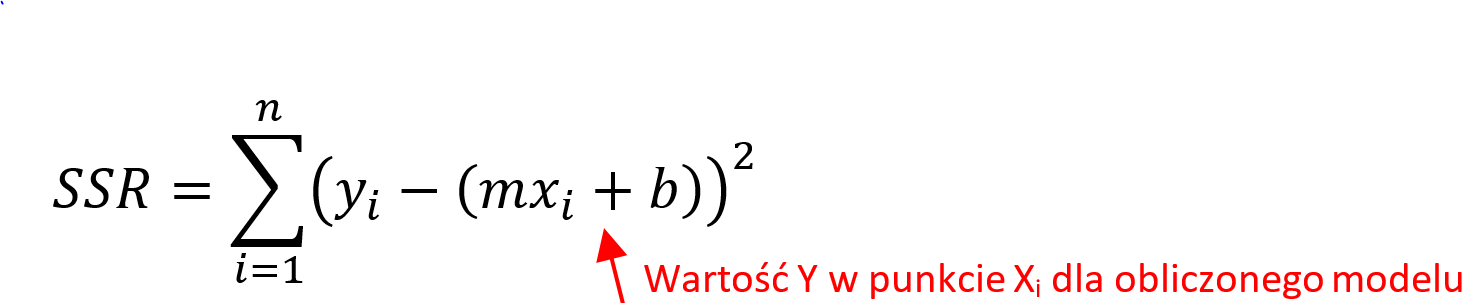
a całkowita suma kwadratów jest opisana wzorem:

Interpretacja geometryczna

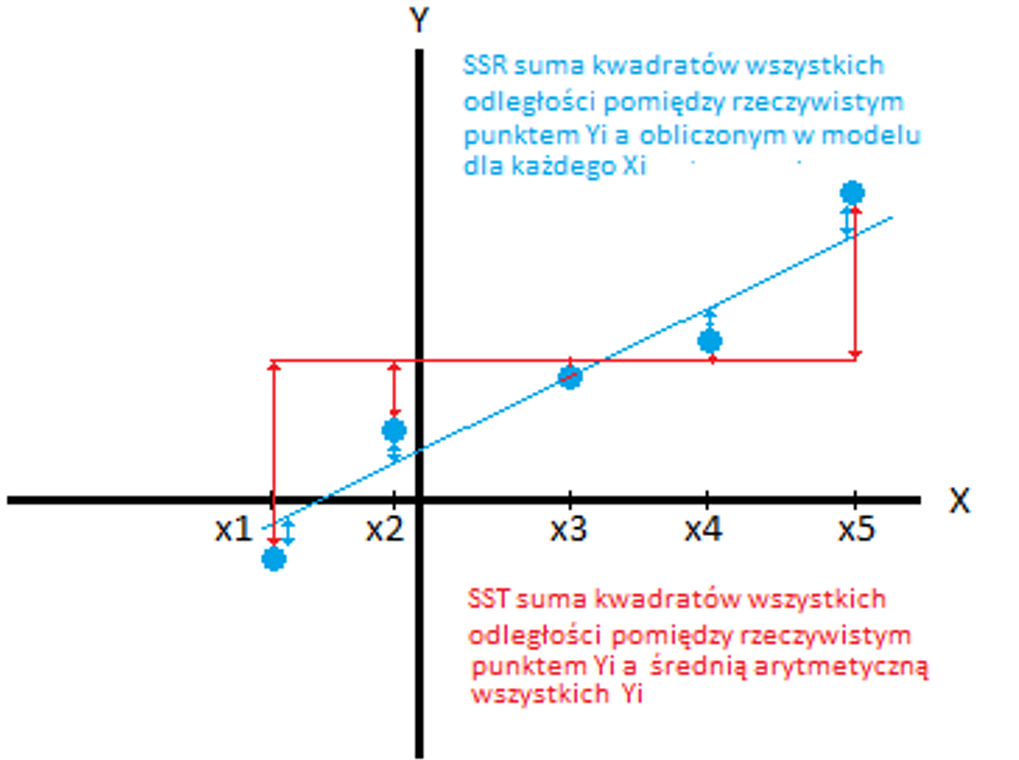
Jak należy interpretować wyniki R² . W zasadzie otrzymane wyniki powinny znajdować się w przedziale R₊ [1, 0]. W praktyce wartość „1” oznacza 100% zgodności naszej predykcji ze zbiorem danych. Oczywiście to przypadek idealny, ale co do zasady wynik 90% i wyższy to oznacza obliczenie predykcji z bardzo dużym stopniem pewności. Odwrotnie, jeśli nasz wynik jest równy zeru to dopasowanie jest żadne.

Pozostają jeszcze do interpretacji dwa przypadki

• R2 osiąga wartość ujemną
• SST jest równe zero

R2<0 – Ze względów praktycznych najniższe R2, jakie można uzyskać, to zero, ale tylko dlatego, że założenie jest takie, że jeśli nasza obliczona linia regresji nie jest lepsza niż średnia arytmetyczna to nie jest dopasowana i procentowo dopasowanie jest równe 0% czyli go nie ma.

 Twierdzenie, że wartość R2 musi być większa lub równa zero, opiera się na założeniu, że jeśli uzyskamy ujemną wartość R2, to trzeba odrzucić wszelkie obliczenia regresji i zastosować wartość średnią. Ujemny R2 oznacza, że nasze dopasowanie jest gorsze niż średnia arytmetyczna.

Oczywiście możemy dla własnych potrzeb przyjąć, że jednak zsumowany błąd kwadratowy nie jest miarą, która ma znaczeni i to jest OK. (na przykład może większe dla nas ma znaczenie błąd bezwzględny zamiast R2)

SST=0 jest to szczególny przypadek, kiedy wszystkie punkty (o ile są) leżą na osi X co oznacza, iż mamy przypadek linii horyzontowej (poziomej) który jest jednocześnie nasza osia X. Ten problem wymaga innego podejścia w matematycznego (badanie wartości R2 w otoczeniu punktu ”0”).  W naszych rozważaniach wystarczy pamiętać, że jest to przypadek szczególny (niezdefiniowany) i o ile mamy taki przypadek to wystarczy wiedzieć że nasza funkcja ma postać y=0 dla dowolnego x z przedziału X∈R(-∞ ; +∞).

Skoro potrafimy oszacować dokładność naszej funkcji to powracając do naszego przykładu z lodami obliczmy nasza regresje dla omawianego przypadku:

Algorytm

• Dane wejściowe najlepiej przygotować w tabeli w taki sposób by po lewej stronie umieścić atrybuty po prawej wartości.
• Dane wyjściowe obliczone współczynniki „m” oraz „b”
• Wykonaj kolejne kroki
  • Oblicz wartość nachylenia „m” oraz wartość przesunięcia „b” zgodnie ze wzorem

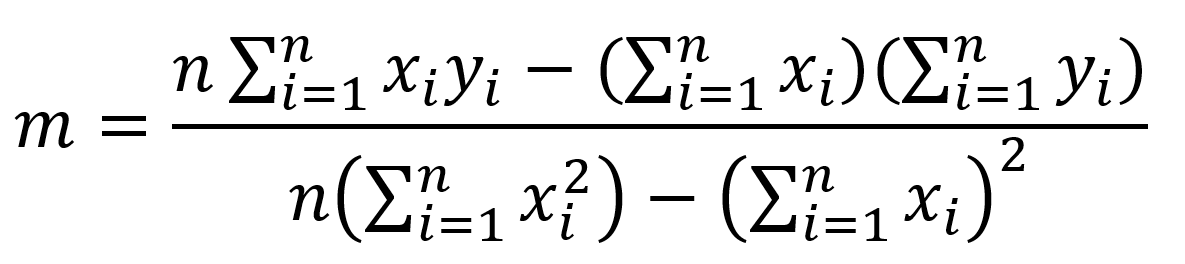
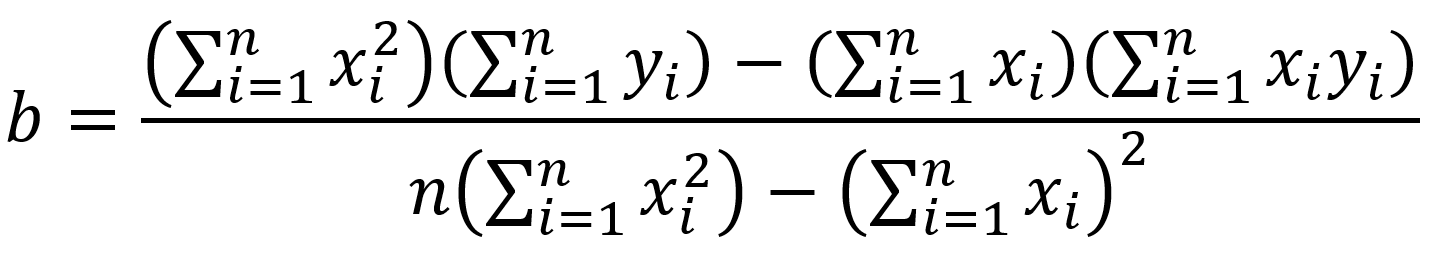
• Oblicz współczynnik determinacji R2 i oszacuj poprawność wyników w zależności od potrzeb

• Jeśli wynik jest niesatysfakcjonujący przeanalizuj dane wejściowe.

Kompletny zestaw obliczeń dla naszego przypadku w Excel tutaj.

Klasyfikator Naive Bayers

Informacje ogólne

Najważniejszą cechą często wskazywaną jako istotną różnicę klasyfikatora Naive Bayes jest stosowanie tego klasyfikatora nie na danych liczbowych a na danych kategoryzyjących. W takim środowisku danych Naive Bayes jest zdecydowanie bardziej wydajny od większości innych klasyfikatorów. Kategoryzacja danych opiera się na prawdopodobieństwie warunkowym jako przesłanki wyboru i w oparciu o różne atrybuty x₁, x₂, x₃…x_n dla każdej próbki istnieje możliwość obliczenia każdej możliwej klasy.

Twierdzenie Bayes’a opisane jest równaniem

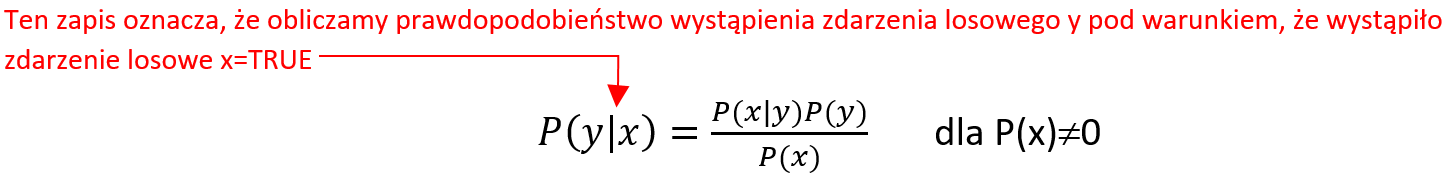
        dla P(x)¹0

Przedstawiony powyżej wzór jest dla jednej klasy i jednego związanego z nią atrybutu. W przypadku kiedy mamy więcej niż jedno prawdopodobieństwo atrybutu, P(x₁), P(x₂,), P(x₃)… P(x_n) to dla każdej klasy y_k  prawdopodobieństwo od atrybutów x₁, x₂, x₃…x_n możemy opisać wzorem:

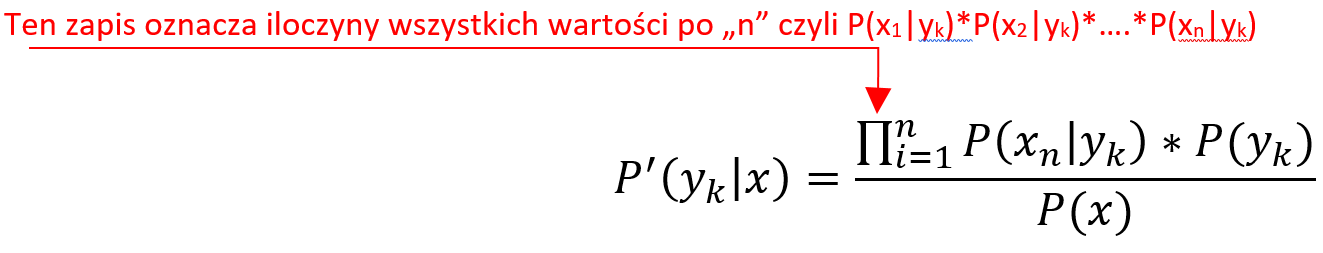
Zatem dla wielu atrybutów i po uwzględnieniu, że licznik i mianownik upraszcza się, ponieważ oba dzielą się przez P(x) do obliczenia po podstawieniu otrzymujemy następujący wzór końcowy:

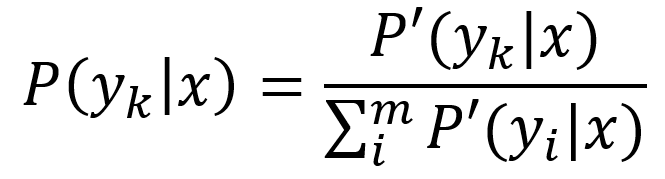
gdzie „m” to liczba kategorii atrybutu.

Podsumowując koniecznie przy obliczaniu prawdopodobieństwa warunkowego musimy pamiętać, że obliczamy prawdopodobieństwo czegoś i nie ma tu znaczenia czy mówimy o elemencie negatywnym, pozytywnym, czy np. neutralnym itd. Mówimy o obliczeniach jako celu jak np. 5 skrzyżowań pod rząd z zielonym światłem, czy 4 kontrole radarowe przez policję na odcinku 100km danej trasy. W obu przypadkach, dla obliczanego prawdopodobieństwa warunkowego jest to obliczenie danego prawdopodobieństwa warunkowego i nic więcej bez względu na to jaki mamy do tych dwóch przypadków stosunek personalny.

I ostatnia uwaga – ogólnie możemy powiedzieć, że twierdzenie Bayes’a w zasadzie oszacowuje nasza hipotezę na podstawie dostarczonych dowodów

Przykład prostego obliczenia prawdopodobieństwa warunkowego.

Jest wzmożony okres zachorowań na grypę. Właśnie mamy ból gardła i boli nas głowa i zakładamy, że pewnie mamy grypę, ponieważ zgodnie z informacją 90% przypadków grypy objawia się w fazie wstępnej właśnie tymi objawami (to tzw. Fałsz Stawki Podstawowej).

Przejrzyjmy więc wszystkie dostępne informacje (Dowody jakie mamy pozyskane z publikacji)

Dowód 1.  90% osób mających grypę miało te same objawy
Dowód 2. Z danych statystycznych wiemy, że w naszym kraju średnio rocznie na grypę choruje ok. 5% populacji
Dowód 4. Z danych statystycznych wiemy, że rocznie do lekarzy z bólem gardła i bólem głowy zgłasza się średnio rocznie 20% populacji

Hipoteza. Chcemy wiedzieć jakie jest prawdopodobieństwo, że mamy grypę. Dla lepszego zrozumienia zmodyfikujemy wzór podstawowy dla jednej klasy:

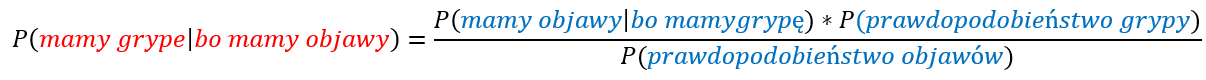
Postawmy nasze dane do wzoru:

HIPOTEZA: P(że mamy grypę)=(90%*5%)/20%= 0,9*0,05/0,2=0,225

Tak więc, prawdopodobieństwo, że mamy grypę wynosi 22,5%. Oczywiście mamy tutaj jedną klasę, ale czynników składowych może być znacznie więcej.

Załóżmy następujący scenariusz. Mamy zestawienie danych z analizy obrazu diagnozowań raka płuc, gdzie możliwość wystąpienia nowotworu oceniana jest na podstawie atrybutów. 10 różnych lekarzy na podstawie tego samego zdjęcia odznaczyło następujące atrybuty

1. Rozmiar komórki zdeformowanej,
2. Ilość komórek zdeformowanych na badaną jednostkę,
3. Obszar zajmowany przez zdeformowane komórki

Przy czym w naszym przypadku każdy z atrybutów posiada dwie wartości. Należy zauważyć, że nasze dane przedstawione są w postaci kategorii, o ile w podobnych obliczeniach pojawiają się dane liczbowe to należy je skategoryzować przed dokonaniem obliczeń. Nasza hipoteza jest następująca: chcemy wiedzieć jak duże jest prawdopodobieństwo, że diagnoza ma wynik pozytywny, mówiąc prościej chcemy wiedzieć jak bardzo jednoznaczna jest diagnoza na podstawie opinii 10 lekarzy.

Tabela jak i wszelkie obliczenia przykładowe w pliku excel tutaj.

Klastrowanie

Uczenie nienadzorowane – klątwa wymiarowości

Klątwa wymiarowości odnosi się do sytuacji, w której mamy dużą liczbę cech, często setki lub tysiące, które prowadzą do niezwykle dużej przestrzeni z rzadkimi danymi, a w konsekwencji do anomalii odległości. Na przykład przy dużych wymiarach prawie wszystkie pary punktów są jednakowo oddalone od siebie; w rzeczywistości prawie wszystkie pary mają odległość bliską średniej odległości. Innym przejawem klątwy jest to, że dowolne dwa wektory są prawie ortogonalne, co oznacza, że wszystkie kąty są bliskie 90 stopni. To praktycznie sprawia, że pomiar odległości jest bezużyteczny. Lekarstwo na przekleństwo wymiarowości można znaleźć w jednej z technik redukcji danych, w której chcemy zmniejszyć liczbę cech, na przykład możemy uruchomić algorytm wyboru cech, taki jak ReliefF, lub algorytm redukcji cech, taki jak PCA.

Uczenie nienadzorowane- klastrowanie (grupowanie)

Klastrowanie (grupowanie) to technika grupowania podobnych danych (danych, których zdefiniowane przez analityka cechy są wzajemnie zbieżne) w klastry według pewnych miar odległości. Główną ideą jest umieszczenie instancji, które są podobne (to znaczy blisko siebie) w tym samym klastrze, przy jednoczesnym zachowaniu niepodobnych punktów (czyli tych bardziej oddalonych od siebie) w różnych skupieniach. Przykład tego, jak mogą wyglądać klastry, pokazano na poniższym diagramie:

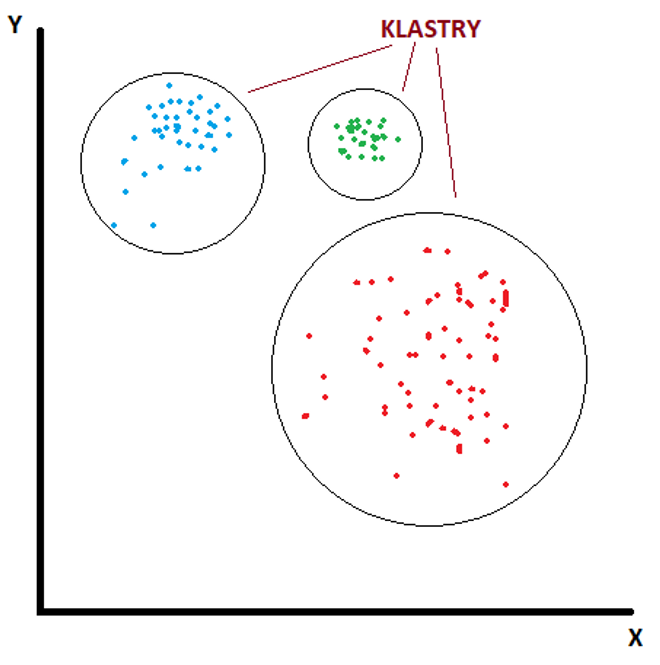
Klastry definicja ogólna

Upraszczając klastry czy klastrowanie to wyszukiwanie zbiorów o podobnych cechach. Operacyjna definicja klastra polega na tym, że biorąc pod uwagę reprezentację n obiektów, gdzie w naszym diagramie są to wszystkie zielone, czerwone i niebieskie punkty trzeba znaleźć grupy na podstawie miary podobieństwa, takiej że obiekty w tej samej grupie są podobne, ale obiekty w różnych grupach nie są takie same. W naszym przypadku podobieństwem są kolory obiektów i takich grup (klastrów mamy 3. Jednak pojęcie podobieństwa można interpretować na wiele sposobów. Klastry mogą różnić się kształtem, rozmiarem położeniem i gęstością konkretna cechą wektora (np. w jednej grupie wektory[a,0,0] w drugiej [0,b,0] itd.) . Klastry są wzorcami i może istnieć wiele rodzajów wzorców. Niektóre klastry to tradycyjne typy, takie jak punkty danych wiszące razem np. na płaszczyźnie 2D (konstelacje). Istnieją jednak inne skupienia, takie jak wszystkie punkty reprezentujące obwód koła czy kwadratu. Mogą istnieć koncentryczne okręgi z punktami różnych okręgów reprezentującymi różne skupiska. Obecność szumu w danych sprawia, że wykrywanie klastrów jest jeszcze trudniejsze. Idealny klaster można zdefiniować jako zbiór punktów, który jest zwarty i izolowany. W rzeczywistości klaster to podmiot subiektywny, którego znaczenie i interpretacja wymaga wiedzy dziedzinowej.

Klastry – sposoby dobierania reprezentantów klastra

Klastry mogą być reprezentowane przez wartość centralną lub modalną (modalna, czyli taką która występuje najczęściej).

• Centralnie tzn. klaster można zdefiniować jako środek ciężkości zbioru punktów, które do niego należą. Centroid jest miarą tendencji centralnej. Jest to punkt, w którym suma kwadratów odległości ze wszystkich punktów jest minimum w tym przypadku korzystamy z definicji odległości Euklidesowej i poszukujemy punktu centralnego konstelacji. Rzeczywistym odpowiednikiem byłoby centrum miasta jako punkt, który jest uważany za najłatwiejszy w użyciu dla wszystkich części składowych miasta. Zatem wszystkie miasta są definiowane przez ich centra lub obszary śródmiejskie.
• Modalnie tzn. klaster jest reprezentowany przez najczęściej występującą wartość w klastrze, tj. Klaster można zdefiniować poprzez jego wartość modalną. W tym przypadku głównym zadaniem jest analiza jaką metodę „odległości” zastosujemy do selekcji grup modalnych.

Techniki grupowania

Analiza skupień to technika uczenia maszynowego. Jakość wyniku grupowania zależy od algorytmu funkcji odległości i aplikacji. Najpierw należy rozważyć jaka funkcję odległości zastosujemy. Większość metod analizy skupień wykorzystuje miarę odległości do obliczania bliskości między parami elementów. Istnieją dwie główne miary odległości: odległość euklidesowa („w linii prostej” lub linia prosta) jest najbardziej intuicyjną miarą. Inną popularną miarą jest odległość Manhattanu (prostoliniowa), gdzie można jechać tylko w kierunkach prostopadłych. Odległość euklidesowa jest przeciwprostokątną trójkąta prostokątnego, podczas gdy odległość Manhattan jest sumą dwóch odnóg trójkąta prostokątnego. Istnieją inne miary odległości, takie jak omówione odległość Jaccarda (do pomiaru podobieństwa zbiorów) lub odległość Levenshteina edycji (podobieństwo tekstów) i inne. Kluczowy cel algorytmu grupowania jest taki sam: jak najlepsze wyizolowanie klastrów ze zbioru danych. Porównywanie algorytmów klastrów jest trudnym zadaniem, ponieważ nie ma jednej prawidłowej liczby klastrów. Jednak szybkość algorytmu i jego wszechstronność pod względem różnych zbiorów danych są ważnymi kryteriami. W ramach tego blogu przedstawione zostaną najczęściej używane metody grupowania zbiorów. Będą to algorytmy wyszukiwania skupień

• Metodą k-średnich (k-means)
• Metodą EM (Expectation–Maximization algorithm)

Klastrowanie metodą K-średnich

Klastrowanie metoda k-means (k-srednich)

Przy klastrowaniu metoda k-means stosuje się prostsze i nie matematyczne podejście do ustawiania ilości klastrów „k” przy ustalaniu domen. Na przykład, jeśli analizujemy dane dotyczące odwiedzających dla witryny sieci web dużego dostawcy usług IT, można przyjąć ustawienie k na 2. Dlaczego dwa klastry? Ponieważ z doświadczenia wiemy, że prawdopodobnie będzie duża rozbieżność w zachowaniu dla zakupów między powracającymi klientami, a nowymi klientami w firmie, która sprzedaje usługi IT. Pierwszy raz odwiedzający rzadko kupują produkty i usługi IT na poziomie docelowych potrzeb swojego przedsiębiorstwa, ponieważ dostawcy usług IT zwykle przechodzą przez długi proces badań i weryfikacji przed zatwierdzeniem dużego zamówienia. W związku z tym można użyć grupowania dwóch k-średnich, aby utworzyć dwa klastry i przetestować moją hipotezą. Po utworzeniu dwóch klastrów można chcieć zbadać jedną z nich poprzez kolejne dwa klastry dalej, albo stosując inną technikę, albo ponownie używając grupowanie k-means od początku z trzema klastrami. Na przykład chcemy podzielić powracających użytkowników na dwie części – nowe klastrowanie (przy użyciu grupowania k-średnich), aby sprawdzić hipotezę, że użytkownicy mobilni vs użytkownicy komputerów stacjonarnych tworzą dwie różne grupy punktów danych. Znowu stosując wiedzę dziedzinową, na podstawie pracy analitycznej wysnuwam hipotezę, że duże przedsiębiorstwa rzadko dokonują zakupów poprzez urządzenia mobilne.

W efekcie końcowym pracy analityka przyjęte przykłady prac źródłowych prawdopodobnie utworzą trzy dyskretne klastry w oparciu o fakty, które zakładają:

• Ruch organiczny obejmuje generalnie zarówno nowych, jak i powracających klientów, którzy chcą robić zakupy w mojej witrynie (za pośrednictwem preselekcja, np. poczta pantoflowa, wcześniejsze doświadczenia klientów).
• Płatny ruch reklam jest kierowany do nowych klientów, którzy zazwyczaj przybywają na witrynę o niższym poziomie zaufania niż ruch organiczny, w tym potencjalnych klientów, którzy przez pomyłkę kliknęli płatną reklamę trend powie w jakiej technologii lokować inwestycje w reklamie.
• Marketing e-mailowy dociera do obecnych klientów, którzy już zrobili zakupy w witrynie i nie wymaga płatnych reklam

To jest przykład wiedzy dziedzinowej oparty na własnym doświadczeniu analityka, istotny jest dla nas fakt, że skuteczność „wiedzy dziedzinowej” znacząco maleje wraz z liczbą k klastrów. Innymi słowy, domena wiedzy może być wystarczająca do określenia dwóch do czterech klastrów, ale mało prawdopodobne, że tak będzie przy wyborze między 20 a 21 skupiskami.

W przypadku podejścia matematycznego tylko od wiedzy i doświadczenia analityka zależeć będzie jakie przyjąć założenia odnośnie ilości klastrów, nie mniej jednak należy przyjąć, że zasada minimalizacji klastrów jest obowiązująca również tutaj.

Z matematycznego punktu widzenia obliczenia polegają na wyszukiwaniu zbiorów, których poszczególne sumy odległości od centroidów są najmniejsze, obliczenia kończymy gdy kolejne iterakcje nie wnoszą znaczących zmian dla założonej liczby centroidów.

Ogólny algorytm grupowania metodą k-średnich:

Celem grupowania K-średnich jest znalezienie etykiet skupień lub równoważnie wektorów wskaźników skupień (zdefiniowanych w celu zminimalizowania sumy kwadratów w obrębie klastra (WCSS). Ogólny wzór zatem przyjmuje postać:

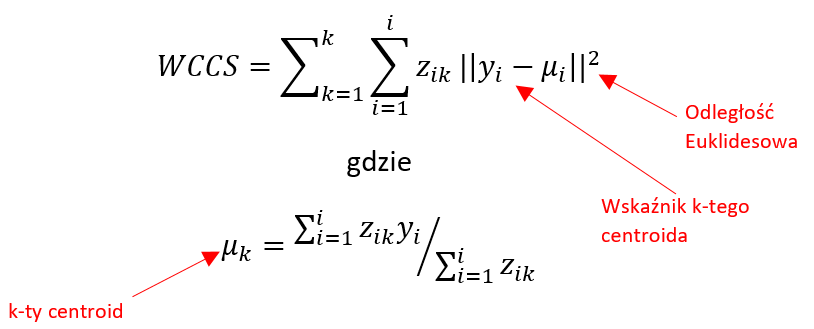
Algorytm

Dane wejściowe. Wybierz zbiór danych Y i dowolną liczbę grup /skupień do utworzenia µ_k– jeden z najważniejszych kroków – wybieramy µ „z buta” ale w przemyślany sposób na podstawie własnych doświadczeń. Istnieją pewne metody optymalizacji tego kroku ale są to rozważanie wykraczające poza zakres informacji podstawowych.

Dane wyjściowe. Zbiór centroidów µ oraz przypisanych do nich zbiorów danych y=f(x).

• Wykonuj w pętli kolejne obliczenia WCCS
• Przypisz obserwacje do klastra i wyszukaj najmniejszej odległości dla danego „k” oraz „i”
  jeżeli

• Oblicz centrum klastra w oparciu o przypisane wartości

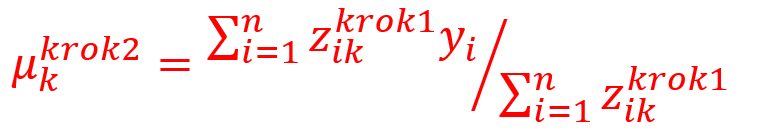
• Powróć do kroku punktu WCCS
• Powtarzaj powyższe kroki, aż różnice zmian pomiędzy pozycjami poszczególnych centroidów będą niezauważalne
• Jeśli klastry nie są satysfakcjonujące, powinno ponownie się przejść do kroku 1 i wybrać inną liczbę grup / segmentów. Tworzenie klastrów może być kontynuowane z inną liczbą klastrów i inną lokalizacją tych punktów. Klastry są uważane za dobre, jeśli definicje klastrów ustabilizują się, a ustabilizowane definicje okażą się przydatne do danego celu.

Przykład EXCEL Opis sytuacji – W koszyku są trzy różne rodzaje owoców mamy określić ile jest owoców o jednocześnie najmniejszej masie (zmienna „z”) i najmniejszej objętości (zmienna „y”).. Zakładany ze k wynosi 2. Zbiór wyszukiwanych owoców musi być skupiony wokół centroida o najmniejszej masie i najmniejszej objętości. Przykładowe obliczenia w excel tutaj.

Klastrowanie metodą EM (maksymalizacji oczekiwań)

Klastrowanie metodą EM (Expectation-Maximization)

Szacowanie największej prawdopodobieństwa to podejście do szacowania gęstości dla zbioru danych poprzez przeszukiwanie rozkładów prawdopodobieństwa i ich parametrów. Jest to ogólne i skuteczne podejście, które leży u podstaw wielu algorytmów uczenia maszynowego, chociaż wymaga, aby zestaw danych szkoleniowych był kompletny, m.in. wszystkie odpowiednie oddziałujące zmienne losowe są obecne. Maksymalne prawdopodobieństwo staje się niewykonalne, jeśli istnieją zmienne, które wchodzą w interakcję z tymi które są już w zbiorze danych, ale zostały ukryte lub nie zostały zaobserwowane, tak zwane zmienne latentne.

Algorytm maksymalizacji oczekiwań jest podejściem do wykonywania estymacji maksymalnego prawdopodobieństwa w obecności zmiennych latentnych. Robi to, najpierw oszacowując wartości zmiennych ukrytych, następnie optymalizując model, a następnie powtarzając te dwa kroki aż do zbieżności. Jest to skuteczne i ogólne podejście, które jest najczęściej używane do szacowania gęstości z brakującymi danymi, takimi jak algorytmy grupowania jak np. Gaussian Mixture Model.

Maksymalizacja oczekiwań zapewnia iteracyjne rozwiązanie estymacji największej prawdopodobieństwa za użyciem zmiennych latentnych.

Modele mieszanin gaussowskich są podejściem do estymacji gęstości, w którym parametry rozkładów są dopasowywane za pomocą algorytmu maksymalizacji oczekiwań. Oznacza to, że algorytm EM jest zdolny do pracy na nieoznakowanych danych w zadaniach niekontrolowanych i gwarantuje, że będzie w końcu osiągał lokalne maksimum lub „wystarczająco dobre” rozwiązanie przybliżenia tego maksimum. Jego użyteczność jest wspierana przez szeroką gamę aplikacji, w tym nieoznakowaną segmentację obrazu, nienadzorowane grupowanie danych, naprawianie brakujących danych lub odkrywanie wyższego poziomu (ukrytej) reprezentacji surowych danych.

Suma prawdopodobieństw od x_i dla z_ij=1   Ogólny algorytm grupowania metoda EM

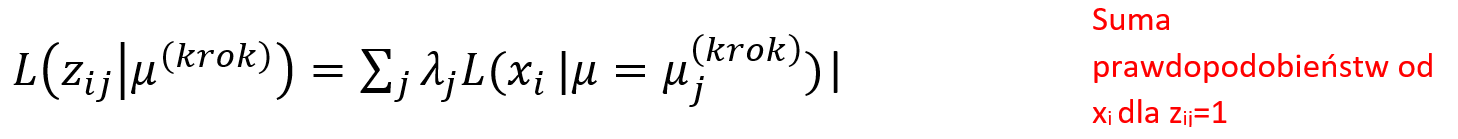
Niech L(x_i|µ^(krok)) oznacza prawdopodobieństwo dla wszystkich „k” takie że:

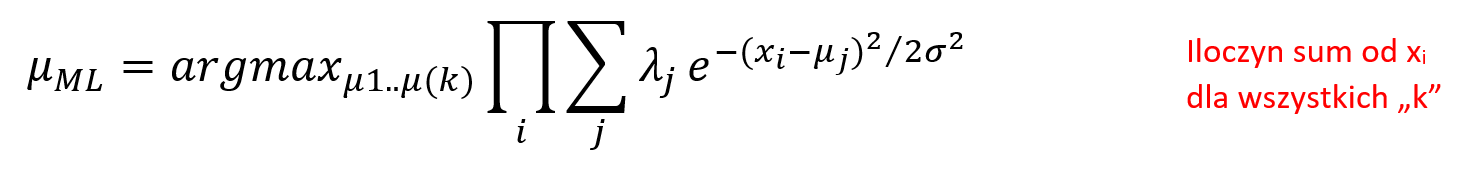
oraz, niech µ_ML oznacza próbę wprowadzenia wartości średnich

Algorytm

Dane wejściowe. Zbiór elementów Y, wstępny podział na „k” grupy oraz elementy wymagane dla obliczeń Gaussowskich – odchylenie standardowe „σ” w obliczeniach najczęściej σ_k=1,punkt rozdziału rozkładów λ_k np. dla k=2, λ₂=0,5. Ponadto przyjmijmy dla poniższych wzorów że „j” będzie indeksem Gaussa, „i” indeksem punktów danych, a „krok” indeksem E-M iteracji.

Dane wyjściowe. Zbiór centrów (maksimów) rozkładu Gaussa „µ”. Wykaz zmiennych powiązanych z danym rozkładem Gaussa. Prawdopodobieństwo danej zmiennej w powiązaniu z „µ” praz „σ”.

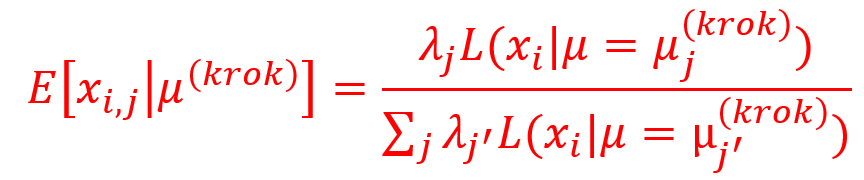
• Wykonaj krok M- Maximization

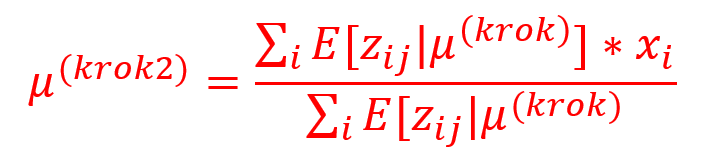
• Powtarzaj kroki od „1” aż wyniki będą mocno zbieżne
  
  

Przykład EXCEL. Skorzystamy z tych samych danych (tym razem tylko 1D po osi x) ale poruszymy inne zagadnienie. Opis sytuacji – dwóch strzelców jeden poczatkujący i jeden klasy mistrzowskiej strzelali do tej samej tarczy. Po zakończeniu testu otrzymaliśmy papierową tarczę i spisaliśmy sobie wszystkie 14 trafień. Mając wiedzę, że były to dwie różne osoby o różnym doświadczeniu spróbujmy oszacować które strzały należały do kogo. W obszarze dane wejściowe C6-C19 spisano wyniki z tarczy. W pierwszym kroku zakładamy, że typowo strzelec µ1 trafiał w okolice „3” (pole H2), a strzelec µ2 trafiał w okolice „8” (pole I2). Obliczeń dokonano w tabeli H5-M19 jako dwie kolejne iterakcje a wyniki przedstawiono w kolumnie O4-O19. Nie wiemy który strzelec oddał ile strzałów, ale z obliczeń wynika ze strzelec początkujący prawdopodobnie trafił 4; 5; 5; 5; 2; 5; 3; 6 a strzelec lepszy prawdopodobnie trafił 8; 7; 10; 8; 10; 10. Co więcej analizując rozkład Gaussa dla µ1=4,38 oraz µ2=8,79 możemy zauważyć, że trafienie „6” jest obarczone podobnym prawdopodobieństwem dla µ1 oraz µ2 co może oznaczać, że strzelec lepszy oddał jeden gorszy strzał i obaj oddali tę sama ilość strzałów. Przykładowe obliczenia w excel tutaj.

Dyskryminacja

Dyskryminacja informacje podstawowe

O dyskryminacji mówimy wtedy gdy wyróżniamy podzbiory danych na podstawie różniących ich cech obserwacji ze znanych podzbiorów cech (dotyczyć to może zarówno populacji jak i próby ale wtedy podzbiory cech mogą się różnić). Stosując dyskryminacje wskazujemy wyróżniki i odpowiadające im wartości liczbowe w taki sposób by wyróżnić lub w pewnym sensie „rozdzielić” badane zbiory.

Przykład: zbiór ludzi stojących w kościele. W tym obszarze na podstawie wyróżnika płeć osoby  możemy wyróżnić i teoretycznie „rozdzielić” podzbiory osób płci żeńskiej oraz osób płci męskiej. Osoby o tych dwóch różnych cechach możemy oczywiście policzyć jako osobne dwie podgrupy chociaż patrząc z zewnątrz widzimy wzajemnie wymieszaną jedna grupę ludzi w jakimś zamkniętym obszarze.

Liniowa analiza dyskryminacyjna (LDA)

Informacje ogólne

LDA jest w pewnym zakresie mieszanką regresji liniowej i klastrowania K-średnich, ale różni się od obu. Grupowanie K-średnich jest nienadzorowaną metodą klasyfikacji, podczas gdy LDA jest nadzorowane, ponieważ jego klasyfikacja jest uczona na znanych danych. Wyniki predykcyjne są ilościowo liczbowe w regresji liniowej, a jakościowo kategoryczne w LDA. Jak wspomniano wcześniej w naszym przypadku regresja jest funkcją która rozdziela podzbiory. Liniowa analiza dyskryminacyjna często jest wykorzystywana do rozpoznawania twarzy w obrazie na podstawie wyuczonych cech szczególnych.

LDA próbuje znaleźć najlepszą funkcję liniową, która może podzielić punkty danych na różne kategorie. Wariancje między średnimi grupowymi powinny być jak największe, podczas gdy wariancje wewnątrz każdej grupy powinny być jak najmniejsze. Wariancje są obliczane po rzutowaniu każdego punktu danych na funkcję liniową o postaci y = a₁x₁ + a₂x₂ + … + a_nx_n + b. Treningowy zbiór danych służy do znalezienia najlepszej reprezentowanej funkcji P przez zestaw parametrów (a₁,a₂,…,a_n,b).

Z powyższych rozważań wynika, iż głównym celem LDA jest redukcja wymiarowości z zachowaniem jak największej ilości informacji po wykonaniu rzutowania. Oznacza to że poszykujemy równania prostej która umożliwi otrzymanie wyniku z jak najlepszym rzutowaniem na nasza prostą  rozdzielającym nasz zbór danych na podzbiory o interesujących nas cechach. Na rysunku poniżej przedstawiono powyższe rozważania z odpowiednimi uwagami.

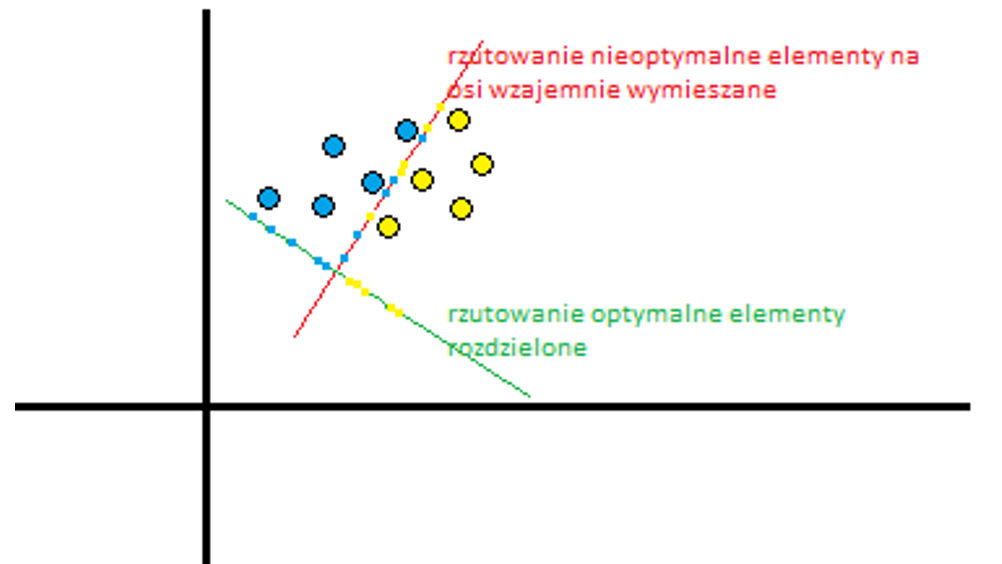
Jak widać rzutowanie prostopadłe na oś oznaczoną kolorem zielonym rozdziela nasze wszystkie punkty według cechy koloru które możemy zdefiniować na określonych odcinkach prostej jako wyodrębnione podzbiory. Odwrotnie dla osi czerwonej nasza cecha koloru jest niejednoznaczna ponieważ punkty rzutu są wzajemnie wymieszane na określonym odcinku prostej w związku z tym nie osiągnęliśmy efektu redukcji wymiarowości.

Algorytm

• Dla danego zestawu danych treningowych, należy zdefiniować zestawy (grupy) cech. które Posortowane na różne grupy, cechy należy dokładnie opisać do dalszej analizy otrzymanych wyników.
• Wykonaj kolejne kroki
• Wykonaj zsumowanie wariancji międzygrupowych za pomocą poniższego wzoru:

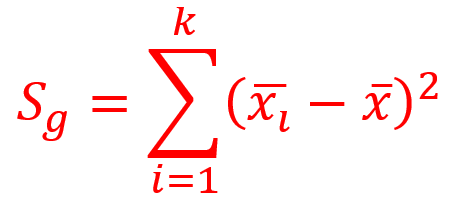
gdzie k to liczba grup, x to średnia ze średnich grupowych, a x_i to średnia indywidualna dla grupy.

• Wykonaj zsumowanie wariancji wewnątrzgrupowych za pomocą poniższego wzoru:

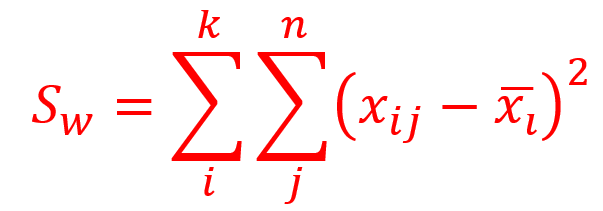
gdzie n to liczba punktów danych w grupie.

• Przyjmując że, P_opt jest najlepszą projekcja rzutowania dla badanego przypadku, rozwiąż równanie poprzez dobór parametrów a₁,a₂,…,a_n,b tak, by osiągnąć maximum ilorazu S_g/S_w:

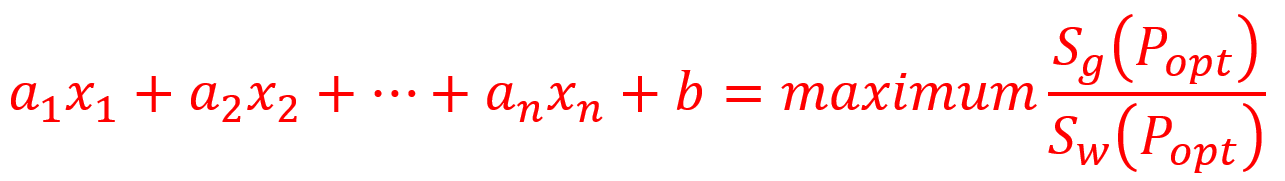
Przykład: Niech zbiorem danych będzie powszechnie znany zbiór danych charakteryzujący gatunki kwiatów Iris. Zbiór posiada 4 atrybuty i 3 stany wynikowe dla wymienionych atrybutów. Nasze zadanie to wyznaczyć optymalne LDA dla przyjętego zbioru danych.

Obliczenia i wyjaśnienia zawarte w pliku excel tutaj.

Sztuczne sieci neuronowe

Wprowadzenie do sztucznych sieci neuronowych

Sieci neuronowe są częścią tzw. głębokiego uczenia, jest gałąź uczenia maszynowego, która okazała się cenna w rozwiązywaniu trudnych problemów, takich jak rozpoznawanie rzeczy na obrazach czy przetwarzanie języka.

Sieci neuronowe mają inne podejście do rozwiązywania problemów niż konwencjonalne programy komputerowe. Aby rozwiązać problem, konwencjonalnie oprogramowanie wykorzystuje podejście algorytmiczne, tj. komputer podąża za zbiorem instrukcji w celu rozwiązania problemu. W przeciwieństwie do tego, sieci neuronowe podchodzą do problemów w bardzo odmienny sposób:

próbując naśladować działanie neuronów na podobieństwo rzeczywistych procesów zachodzących w mózgach istot żywych. W rzeczywistości uczą się przez przykład, zamiast być zaprogramowanym od początku do końca obiektem do wykonania określonego zadania.

Technicznie składają się one z dużej liczby połączonych ze sobą elementów przetwarzania (węzły), które działają równolegle, aby rozwiązać specyficzny problem, który w sposobie przetwarzania danych jest podobny do działania mózgów istoto żywych. Z technicznego punktu widzenia możemy wyodrębnić pewną ogólne grupę cech sztucznych sieci neuronowych.

Sieci neuronowe są specyficzne dla rozwiązywanego zagadnienia: Sieci neuronowe są zawsze budowane w celu rozwiązania określonego rodzaju problemu, chociaż nie oznacza to, że mogą być używane jako narzędzia „ogólnego przeznaczenia”. Na przykład, nie ma algorytmu „ogólnego przeznaczenia”, w którym można ulokować każde dane w celu ich przewidywania lub szacowania, lub, może inaczej, nie znalazłem jeszcze niczego takiego w dostępnej literaturze. Przykłady konkretnych zastosowań obejmują: przewidywanie, prognozowanie, szacowanie, klasyfikację i rozpoznawanie wzorców. Przykłady ze świata rzeczywistego obejmują np. prognozy giełdowe, wycenę nieruchomości, diagnozę medyczną, rozpoznawanie pisma ręcznego czy rozpoznawanie obrazów.

Sieci neuronowe mają zasadniczo trzy podstawowe części: sieć neuronowa ma trzy podstawowe sekcje lub części, a każda część składa się z „węzłów”.

• Warstwa węzłów wejściowych (w tym również węzeł skrośny)
• Ukryte warstwy węzłów przetwarzania (tych warstw może być jedna lub więcej w zależności od stopnia złożenia rozwiązywanego problemu połączone krawędziami wzajemnie i warstwami wejścia i wyjścia).
• Warstwa wyjściowa (wyjściem może być jeden węzeł lub więcej)

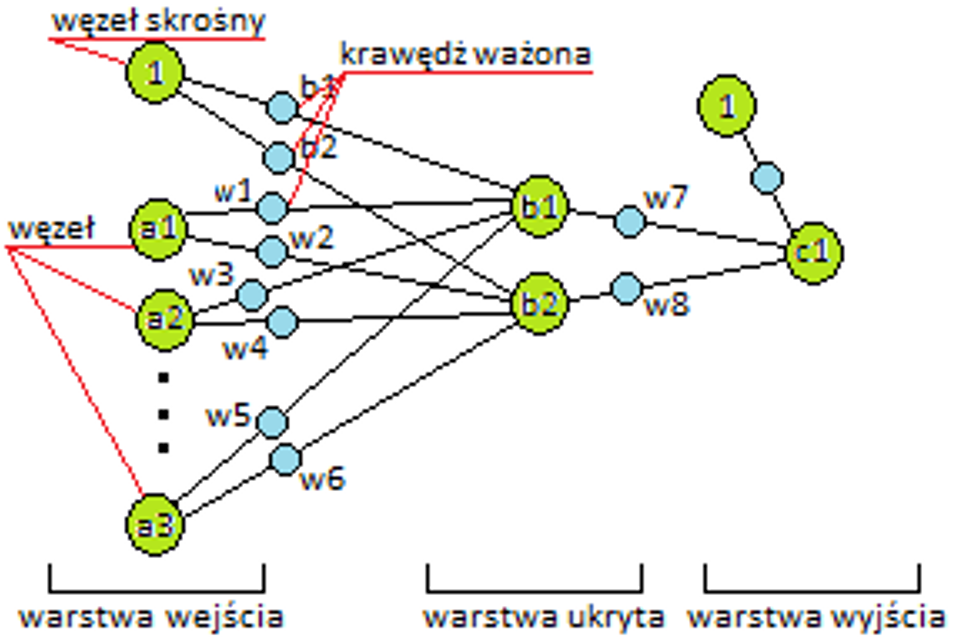
Sieci neuronowe w zakresie logiki przejścia sygnału rozróżniają się na dwie metody przetwarzania sygnału:

• Ze sprzężeniem(postępem) w przód (feedforward) : W przypadku sieci neuronowej ze sprzężeniem do przodu sygnały przemieszczają się tylko w jedną stronę, od wejścia do wyjścia. Tego typu sieci są prostsze i powszechnie stosowane w odniesienia do wzorca, gdzie istotne jest szybkie rozpoznanie badanego obiektu do wyuczonego wzorca. Konwulsyjna sieć neuronowa (CNN lub ConvNet) to specyficzny typ sieci sprzężenia zwrotnego, która jest często używana np. w rozpoznawaniu obrazów.
• Ze sprzężeniem zwrotnym (feedback) nazywane tez jako powtarzające się sieci neuronowe, RNN: W przypadku RNN sygnały mogą przesyłać obie strony kierunkach i mogą działać w pętlach. Sieci sprzężenia zwrotnego są potężniejsze i bardziej złożone niż CNN i zawsze się zmieniają. Sieci RNN są rzadziej używane, niż sieci ze sprzężeniem do przodu, po części dlatego, że algorytmy uczenia dla układów sieci w konfiguracji RNN są (przynajmniej obecnie) znacznie bardziej skomplikowane do uruchomienia i testowania od strony matematycznej (reinforced learning). Sieci RNN ​​są niezwykle interesujące i są znacznie bliższe w duchu do tego, jak działają mózgi istot żywych, niż sieci z postępem w przód.

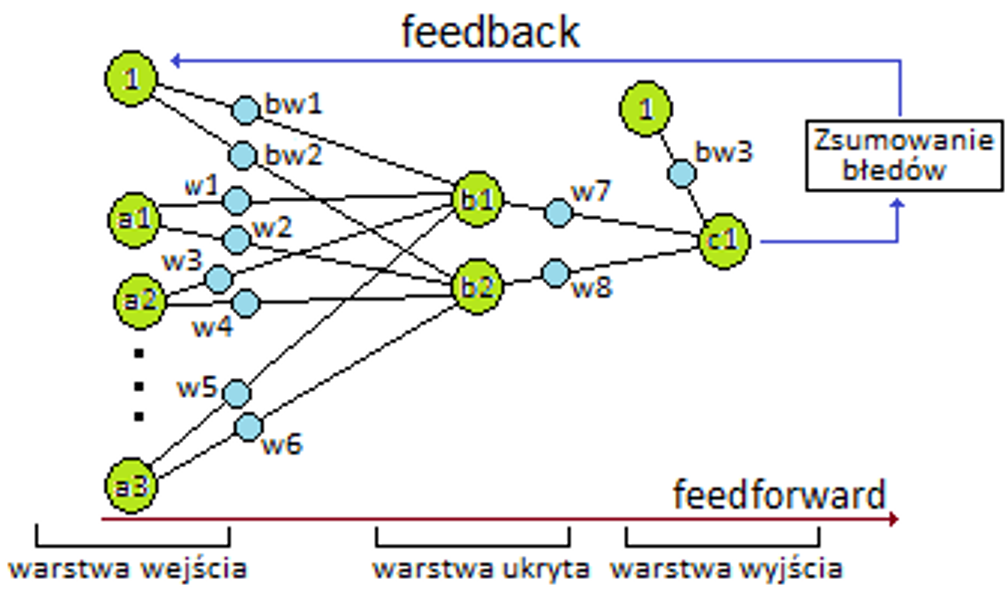
Sieci neuronowe są albo stałe, albo adaptacyjne: Sieci neuronowe pod względem typu wag krawędziowych dzielimy na:

• Stała: Wartości wag w sieci stacjonarnej pozostają statyczne. Nie zmieniają się.
• Adaptacyjna: Wartości wag w sieci adaptacyjnej nie są statyczne i mogą się zmieniać.

Sieci neuronowe wykorzystują trzy typy zestawów danych: Sieci neuronowe są często budowane i trenowane przy użyciu trzech zestawów danych:

• Zestaw danych uczących: Zestaw danych uczących służy do dostosowania wag sieci neuronowej.
• Zestaw danych walidacyjnych: Zestaw danych walidacyjnych służy do zminimalizowania problemu zwanego przepełnieniem, który omówimy bardziej szczegółowo.
• Zestaw danych testowych: testowy zestaw danych jest używany jako ostateczny test, aby ocenić, jak dokładnie sieć została przeszkolona.

Typowy podział danych jest stosunkowo zbieżny do cross validation chociaż dla sieci neuronowych „złoty standard” danych pobranych z jednego bloku to:

• Dane treningowe: 60%
• Dane walidacyjne: 20%
• Dane testowe: 20%.

Warstwa wejściowa

Węzeł wejściowy zawiera dane wejściowe sieci i to wejście jest zawsze numeryczne. Jeśli wejście nie jest domyślnie numeryczne, zawsze badany obiekt należy sprowadzić do postaci numerycznej.
Przykład:
Obrazy są często konwertowane do skali szarości, a każdy piksel jest mierzony w skali od 0 do 1 dla intensywność (gdzie 0 (zero) to kolor czarny, a 1 to kolor biały).
Tekst jest konwertowany na liczby. Na przykład mężczyzna/kobieta może zostać przekonwertowany na 1 i 0 (zero).
Dźwięk jest konwertowany na liczby, które reprezentują amplitudę w czasie, z 0 (zero), gdy dźwięk jest skwantowany jako najcichszy i 1, gdy jest głośno.
Węzeł wejściowy znajduje się w warstwie wejściowej, która jest pierwszą warstwą sieć neuronowa. Każdy węzeł wejściowy reprezentuje pojedynczy wymiar i jest często nazywany elementem, a wszystkie elementy są przechowywane w wektorze.
Przykład, jeśli jako dane wejściowe masz obraz o wymiarach 16×16 pikseli, masz łącznie 256 węzłów wejściowych. Dzieje się tak, ponieważ każdy węzeł wejściowy reprezentuje pojedynczy piksel obrazu, a łącznie jest ich 256 pikseli (16×16). Teraz, w świetle dostępnego języka opisowego, istnieje wiele sposobów opisu wektora wejściowego, w tym np. nasze 256 węzłów dla innych to 256 funkcji albo 256 wymiarów, ale w technice sieci neuronowych to są węzły.

Warstwa ukryta

Ukryta warstwa — ukryta warstwa to warstwa węzłów między warstwą wejściową a warstwą wyjściową. Może być jedna ukryta warstwa lub wiele ukrytych warstw w sieci neuronowej, a im więcej ich istnieje, tym „głębsze” uczenie się. W rzeczywistości wiele ukrytych warstw jest tym terminem opisywanym jako głębokie uczenie (głębokie uczenie nie oznacza tego samego co uczenie reinfoced). Wybór liczby ukrytych warstw to złożony temat i wykraczający poza zakres naszego przeglądu. Elementami warstwy ukrytej są ukryte węzły. Ukryty węzeł to węzeł w ukrytej warstwie. Warstwa może mieć wiele ukrytych węzłów i istnieją różne teorie implementacji prawidłowej ilości. Ogólne zasady będące połączeniem pomiędzy próbą i błędami są tym, czym kieruje większość analityków danych i programistów. Warto odnotować, iż pojawiające się często opinie najczęściej wskazują, że warstwy zawierające taką samą ilość węzłów ukrytych generalnie działały tak samo lub lepiej niż z malejącą lub rosnąc siecią węzłów ukrytych w stosunku do warstwy wejściowej.

Warstwa wyjściowa

Węzeł wyjściowy to węzeł w warstwie wyjściowej. Warstwa wyjściowa może posiadać jeden kub więcej węzłów wyjściowych w zależności od celu zadania i planów programisty. Na przykład, jeśli istnieje sieć służąca do klasyfikowania (rozróżniania) odręcznych cyfr od 0 do 9, byłoby 10 węzłów wyjściowych. W tym przypadku podobnie jak wejście sieci, wyjście jest wektorem.

Krawędź ważona

Waga to zmienna, która znajduje się na krawędzi między węzłami. Wynik każdego węzła w warstwie jest mnożony przez wagę, a następnie zsumowany z innymi ważonymi węzłami w tej warstwie, aby stać się danymi wejściowymi netto węzła w kolejnej warstwie. Wagi są ważne, ponieważ są głównym mechanizmem „strojenia” używanym do trenowania sieci. Krawędziowe algorytmy są zwykle używane do przypisywania losowych wag dla każdego neuronu w sieci. Są różne zakresy wag np. najczęściej -1<->+1.

Węzeł skrośny (odchylenia, wtrącenia – bias node)

Węzeł odchylenia to dodatkowy węzeł dodawany do każdego węzła ukrytego i węzła w warstwie wyjściowej. Węzeł skrośny łączy się z każdym węzłem w każdej odpowiedniej warstwie. Gówna cechą węzła skrośnego jest fakt, że nigdy nie jest połączony z poprzednią warstwą, ale jest po prostu dodawana do węzła danej warstwy. Ponadto zazwyczaj ma stałą wartość np. 1 lub -1 i ma dodana odpowiednia wagę na krawędzi łączącej. Technicznie rzecz biorąc, waga zapewnia każdemu węzłowi w sieci neuronowej możliwość do trenowania ze stałą wartością ( np. 1 lub -1). Na poziomie praktycznym umożliwia to funkcja aktywacji węzła skrośnego, która może wymusić „przesunięcie” przykładowo albo do –1 albo do +1. Obok dostosowania wag, to „przesunięcie” może być bardzo ważne i krytyczne dla osiągnięcia sukcesu w procesie nauczania.

Przykład
Na rysunku poniżej znajduje się przykład wykreślonej funkcji logistycznej (Sigmoida). Dzięki „wtryśnięciu” dodatkowej wartości do węzła możliwe jest  „przesunięcie” sygmoidy po osi X odchylając w lewo lub wprawo od pozycji 0 (zero). W praktyce wartość funkcji y-f(x) dla x=0 może przybierać trzy różne wartości y=0,5 w pozycji przed „dostrojeniem” co może doprowadzić do błędnej decyzji i niejednoznaczności oraz 0 (zero) lub -1 po dostrojeniu patrząc po osi „Y”.

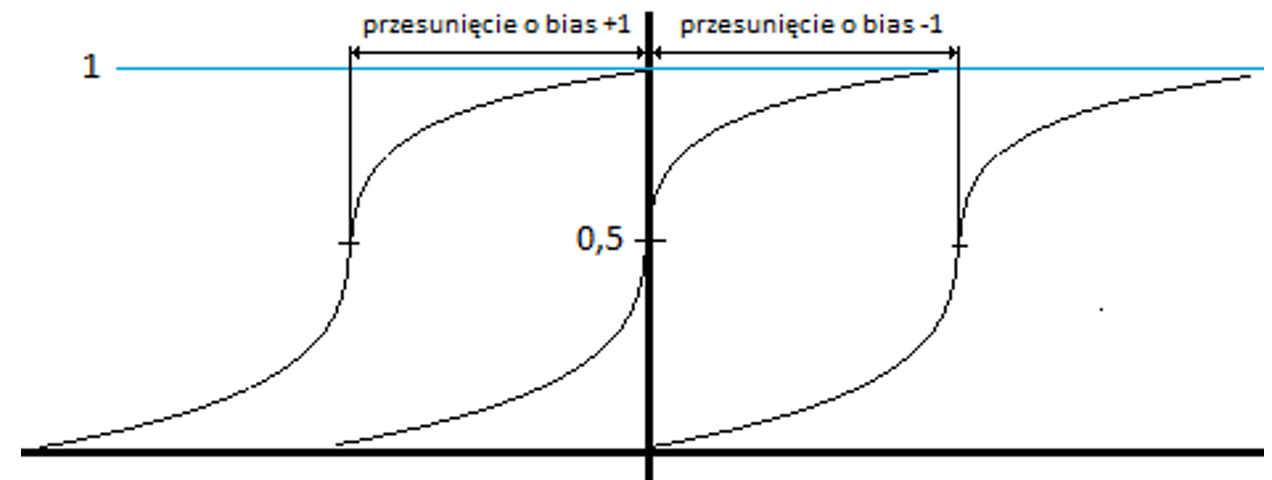
Wskaźnik uczenia się (współczynnik szybkości nauki learning rate)

Współczynnik szybkości uczenia się to wartość, która ocenia tempo uczenia się algorytmu. Z technicznego punktu widzenia określa rozmiar kroku, jaki wykonuje algorytm, gdy zbliża się do globalnego minimum, tj. najniższego poziomu błędu. W praktyce minimum globalne często nie jest osiągane, a algorytm ustawia się na minimum lokalnym, które jest zbliżone do globalnego.

Szybkość uczenia się może być statyczna i pozostawać stała przez cały proces uczenia się lub może być zaprogramowana tak, aby zmniejszała się wraz ze spadkiem współczynnika błędów sieci. Istnieje wiele teorii na temat wyboru odpowiedniego tempa uczenia się ale pewne ogólne zasady spełniają się dla większości przypadków

• Tempo uczenia się najczęściej będzie zależało od przyjętych przez programistę metod prób i korekcji błędów.
• Zbyt wysoki wskaźnik uczenia się może wpłynąć na zdolność sieci do zbieżności – lub innymi słowy, nie osiągnie globalnego minimum i jednoznacznego wyniku. Może to również spowodować przeciążenie sieci i/lub niekontrolowane rozbieżności w wynikach końcowych
• Zbyt niska szybkość uczenia się może powodować, że osiągnięcie  zbieżność wyniku sieci neuronowej może zająć dużo czasu.
• Większość przypadków analiz wskazuje, że wskaźniki uczenia się bliskie 0 (zero), i oscylują wokół wartości 0.1.

Węzły neuronowe od strony matematycznej https://pl.wikipedia.org/wiki/Macierz

Zasadniczo w węźle dokonują się dwie operacje tj. zsumowanie wszystkich informacji wejściowych dochodzących do węzła oraz przemnożenie przez aktywator (funkcję aktywacyjna). Tak wykonana operacja jest tzw. wartością węzła (nauczoną), która w procesie propagacji sygnału przez sieć neuronową będzie w przyszłości służyła do porównywania i innymi danymi wejściowymi w procesie decyzyjnym. Poniższy rysunek przedstawia omówiona koncepcje koncepcję.

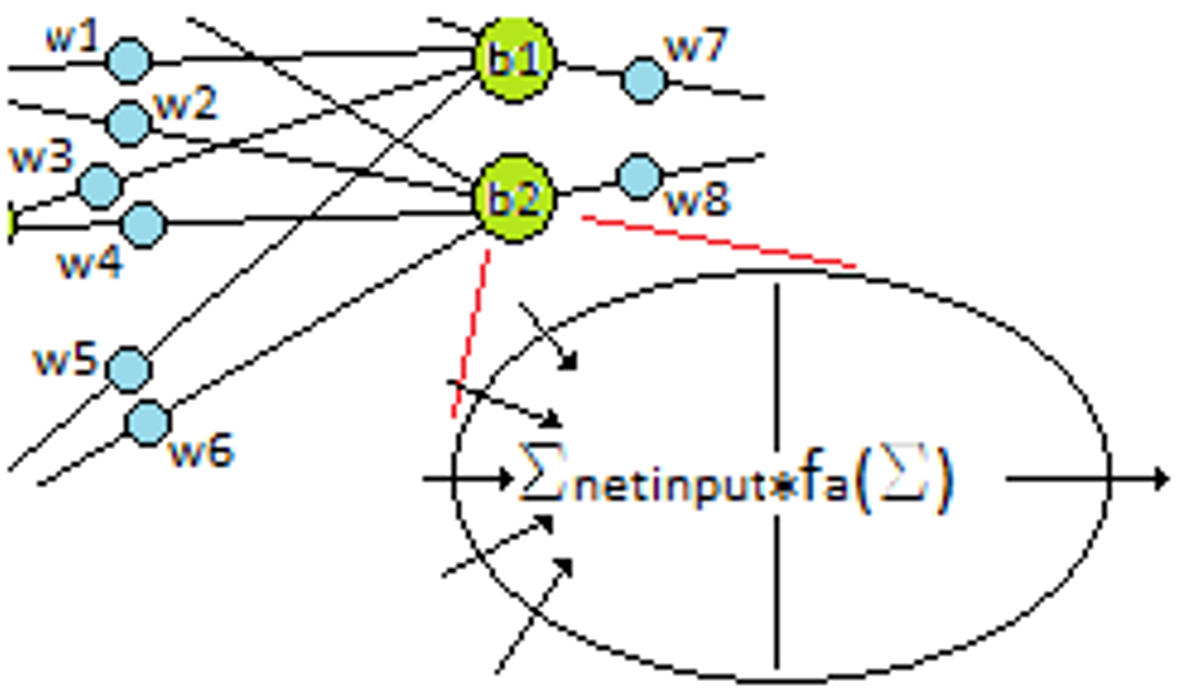
Suma informacji wejściowej (netinput)

Każdy węzeł ukryty w warstwie ukrytej i węzeł wyjściowy w warstwie wyjściowej w sieciach neuronowych może mieć wiele wartości wejściowych. Dla tych wszystkich wartości wejściowych danego węzła tworzone są dane wyjściowe. Podczas wprowadzanie nowego węzła dane wejściowe, muszą być sumowane i przekształcane w jedną wartość wyjściową.  Aby to zrobić, operator sumowania wykorzystuje macierze, a jego wyjście zazwyczaj nazywany iloczynem skalarnym lub iloczynem wewnętrznym. Suma informacji wejściowej najczęściej jest opisywana poniższym wzorem:

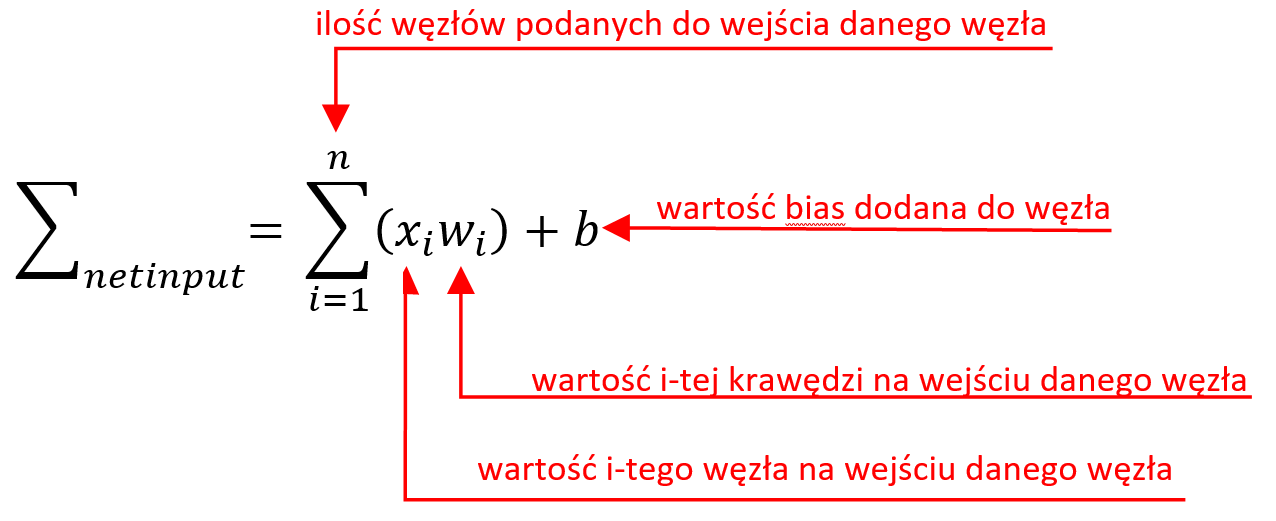
Funkcja aktywacyjna (aktywator)

W sieci neuronowej funkcja aktywacyjna otrzymuje wynik operatora sumowania ( Suma_(netinput) ) i przekształca go na końcowy wynik węzła. Na wysokim poziomie funkcja aktywacjizasadniczo normalizuje dane wejściowe do oczekiwanego zakresu możliwych wartości wyjściowych i przekazuje na wyjście węzła. Przekształcona przez aktywator wartość wyjściowa w swoim wyniku reprezentuje, ile węzeł powinien wnieść w wartości wyjściowej np. wartość liczbowa z przedziału (0; 1); wartość tylko „0” lub „1” logicznie itd. Dobór funkcji aktywatora związany jest z kilkoma czynnikami tj.

• tego jakim zakresem danych wejściowych operujemy (jest to funkcja sumowania , ale niekoniecznie wartości dziesiętnych),
• jaki jest oczekiwany zakres wartości wyjściowych danego węzła,
• jaki jest wpływ danej funkcji aktywacyjnej na szybkość propagacji sygnału poprzez sieć neuronową.
• czy będziemy i w jakim zakresie korzystać z bias. W kontekście bias warto dodać jedna uwagę. Zasadniczo daną sieć neuronową projektuje się dla rozwiązania konkretnego zagadnienia warto w tym miejscu odnotować że stosowanie bias może umożliwić w pewnym zakresie do przełączania zbudowanej sieci rozszerzającą jej funkcjonalności dla zagadnień podobnego typu.
• jaki problem mamy do rozwiązania np. dla problemów nieliniowych bardziej korzystne będą funkcje nieliniowe jak regresja logistyczna czy tangens hiperboliczny. Natomiast dla rozpoznawania obrazów z konwolucyjnymi sieciami neuronowymi (CNN) bardziej korzystna będzie funkcja ReLU. To zagadnienie jest tematem stosunkowo rozległym zarówno od strony matematycznej jak i od strony doświadczalnej. Najprościej można ująć to tak – jeśli rzutowanie LDA (opis w segmencie Dyskryminacja) nie daje dobrych rezultatów i badane klasy trudno jest podzielić linią prostą (rysunek Dyskryminacja LDA), to z bardzo dużym prawdopodobieństwem powinniśmy zastosować np. funkcję sygmoidalną lub tangensa hiperbolicznego w połączniu z wielowarstwowa siecią neuronową.

W poniższej tabeli przedstawiono najbardziej popularne funkcje aktywacyjne gdzie „x” oznacza sumę informacji wejściowej

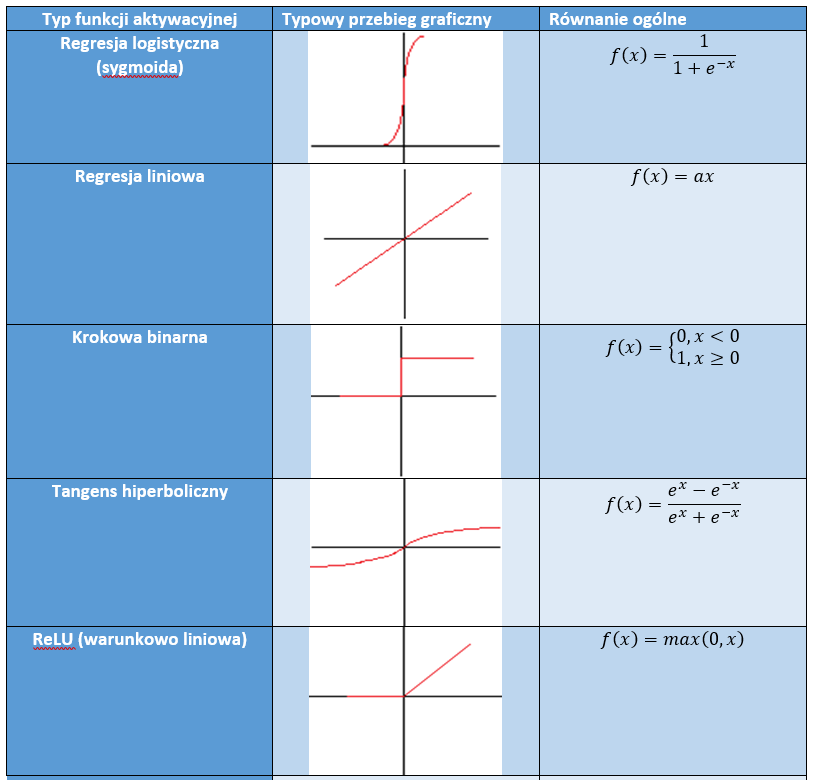
Propagacja sygnału w sieci neuronowej

Jak wspomniano wcześniej równanie węzła można przedstawić w postaci ogólnej jako:

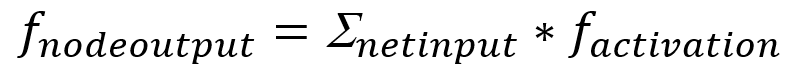
gdzie f_nodeoutput to funkcja wyjściowa węzła; SUMA_netinput to suma informacji wejściowej; a f_activation to funkcja aktywacyjna. Wartość jaka otrzymamy na wyjściu danego węzła to:

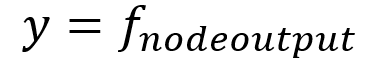
Propagacja do przodu (feedforward) to powtarzalne zadanie. Obliczenie takiej sieci neuronowej polega na wykonaniu obliczeń krok po kroku dla każdego węzła od wejścia do wyjścia poprzez wszystkie warstwy, które zaplanujemy korzystając z funkcji, którą wyprowadziliśmy powyżej. Projekt przykładowy w Excel dla sieci neuronowej z propagacją w przód będzie podzielony na dwa etapy.
Etap 1 (zakładka Etap1) to proces uczenia, gdzie podstawimy obrazy wzorcowe a „zapamiętany wynik” jest przeniesiony do Etap2
Etap 2 (zakładka Etap2), gdzie dokonamy próby „rozpoznania” każdego obrazu.

Dla naszych potrzeb przygotowano dwa „obrazy: w postaci plików *.ico do rozwiązania odwiecznego dylematu „co mamy na obrazku jajko czy kurę”. Dla uproszczenia rachunku skorzystamy 8×8 map bitowych. Obliczamy przykład dla sieci z propagacją do przodu.  W przykładzie wykorzystamy dwie funkcje:

• regresja logistyczna – dla warstwy wejściowej oraz dla warstwy ukrytej
• krokowa binarna – dla warstwy wyjściowej

Jak wspomniano obliczeń dokonano w dwóch etapach. W zakładce Etap1 nasza sieć neuronowa przechodzi proces uczenia się. Wynik obliczeń jest przeniesiony do Etap2 jako wartość BIAS. Nasza sieć neuronowa ma rozróżniać dwa rysunki które dla potrzeb obliczeń przykładowych utworzono jako miniaturowe bitmapy (BMP) o wymiarach 8×8 które z rozszerzeniem *.ICO które są widziane w systemie Windows jako kolorowe ikony z których jedna przedstawia KURĘ a druga JAJO. Nasze „obrazki” zostały przetworzone do postaci cyfrowej i pola z danymi rysunku przeniesione do przykładowego pliku Excel. Zrobiono to poprzez wykorzystanie możliwości podglądu bitowego pliku za pomocą programu NOTEPAD++. Do zrozumienia budowy plików BMP można przeanalizować informacje zawarte w tym linku.
Na rysunku poniżej przedstawiono podgląd pliku za pomocą Notepad++. Widok celowo rozłożono na 18 kolumn by wychwycić pierwsze 54 bajty które nie niosą dla naszego przykładu danych o obrazie są natomiast niezbędne do prawidłowego funkcjonowania pliku BMP w systemie Windows.

Zakreślone dane o obrazie dla obu ikon („obrazów”) zostały przekopiowane do pliku Excel w którym dokonujemy obliczeń. Dane te zostały w Excel przeliczone na postać dziesiętną w ukrytej częściowo kolumnie. W zakładce Etap2 każdorazowo do wykonania obliczeń testowych dane z kolumn KURA  lub JAJO trzeba wkleić do kolumny. Oczywiście można by było to zrobić za pomocą makra ale dla osób początkujących mogłoby to utrudnić zrozumienie procesu. Obliczenia są dostępne w poniższym pliku excel tutaj.